LGCPs - Spatial covariates • inlabru

Set things up

library(INLA)
library(inlabru)
library(fmesher)
library(RColorBrewer)
library(ggplot2)
bru_safe_sp(force = TRUE)
bru_options_set(control.compute = list(dic = TRUE)) # Activate DIC output

Introduction

We are going to fit spatial models to the gorilla data, using factor and continuous explanatory variables in this practical. We will fit one using the factor variable vegetation, the other using the continuous covariate elevation

(Jump to the bottom of the practical if you want to start gently with a 1D example!)

Get the data

data(gorillas_sf, package = "inlabru")

This dataset is a list (see help(gorillas_sf) for details. Extract the objects you need from the list, for convenience:

nests <- gorillas_sf$nests
mesh <- gorillas_sf$mesh
boundary <- gorillas_sf$boundary
gcov <- gorillas_sf_gcov()
#> Loading required namespace: terra

Factor covariates

Look at the vegetation type, nests and boundary:

ggplot() +
  gg(gcov$vegetation) +
  gg(boundary, alpha = 0.2) +
  gg(nests, color = "white", cex = 0.5)

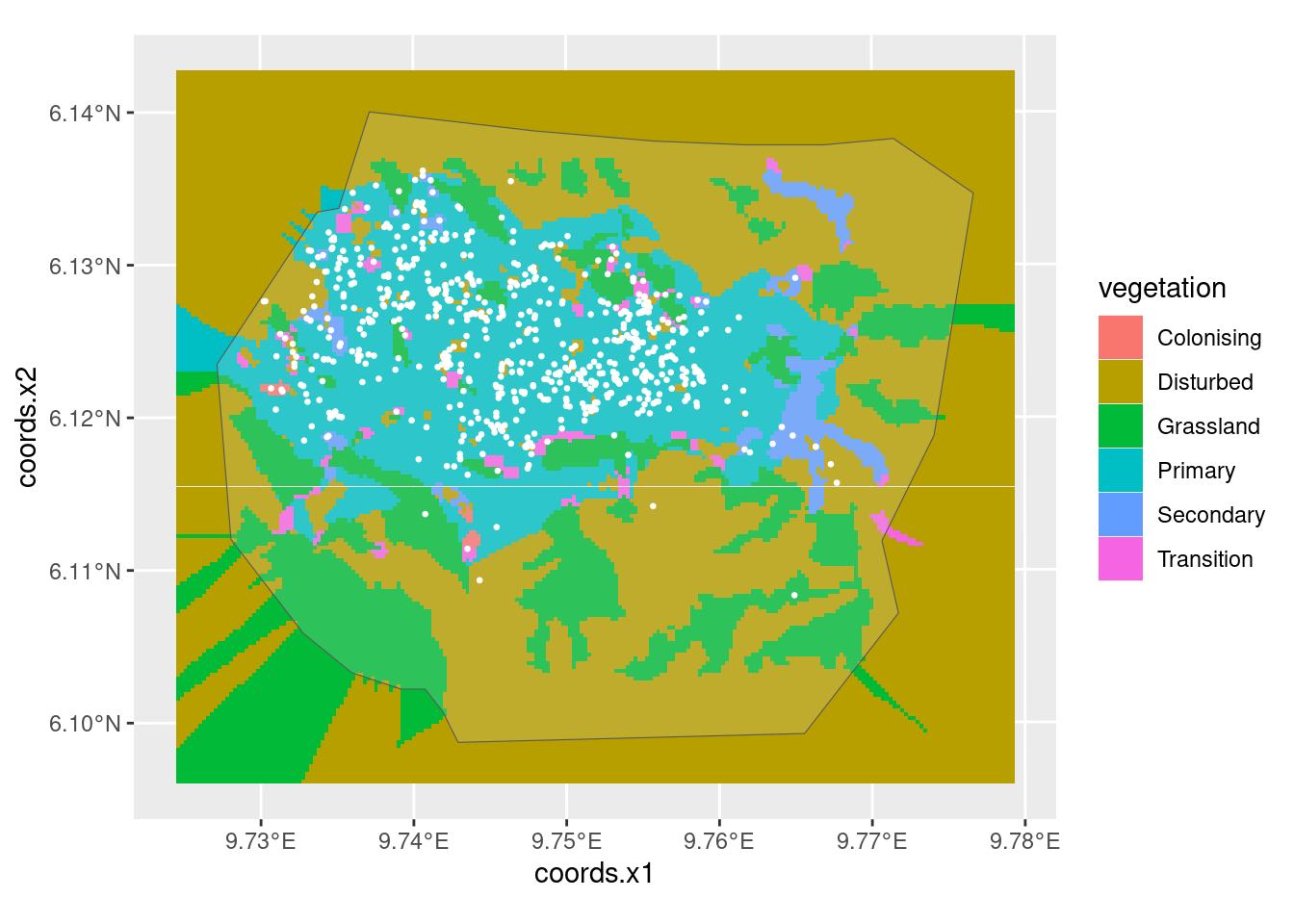
Or, with the mesh:

ggplot() +
  gg(gcov$vegetation) +
  gg(mesh) +
  gg(boundary, alpha = 0.2) +
  gg(nests, color = "white", cex = 0.5)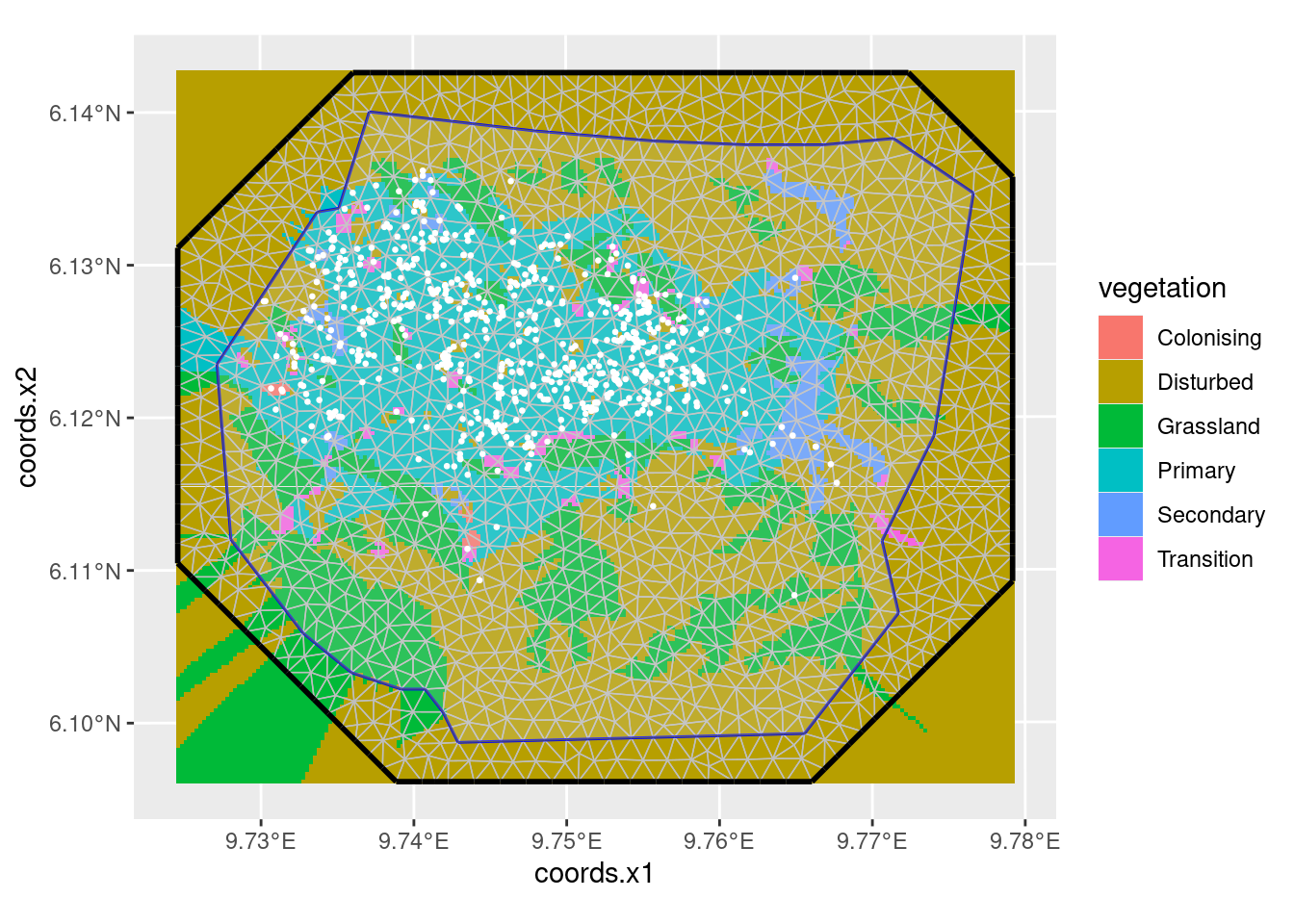

A model with vegetation type only

It seems that vegetation type might be a good predictor because nearly all the nests fall in vegetation type Primary. So we construct a model with vegetation type as a fixed effect. To do this, we need to tell ‘lgcp’ how to find the vegetation type at any point in space, and we do this by creating model components with a fixed effect that we call vegetation (we could call it anything), as follows:

comp1 <- geometry ~ vegetation(gcov$vegetation, model = "factor_full") - 1

Notes: * We need to tell ‘lgcp’ that this is a factor fixed effect, which we do with model="factor_full", giving one coefficient for each factor level. * We need to be careful about overparameterisation when using factors. Unlike regression models like ‘lm()’, ‘glm()’ or ‘gam()’, ‘lgcp()’, inlabru does not automatically remove the first level and absorb it into an intercept. Instead, we can either use model="factor_full" without an intercept, or model="factor_contrast", which does remove the first level.

comp1alt <- geometry ~ vegetation(gcov$vegetation, model = "factor_contrast") +
  Intercept(1)

Fit the model as usual:

fit1 <- lgcp(comp1, nests, samplers = boundary, domain = list(geometry = mesh))

Predict the intensity, and plot the median intensity surface. (In older versions, predicting takes some time because we did not have vegetation values outside the mesh so ‘inlabru’ needed to predict these first. Since v2.0.0, the vegetation has been pre-extended.)

The predict function of inlabru takes into its data argument an sf object or other object supported by the predictor evaluation code (for non-geographical data, typically a data.frame). We can use the inlabru function pixels to generate an sf object with points only within the boundary, using its mask argument, as shown below.

pred.df <- fm_pixels(mesh, mask = boundary)
int1 <- predict(fit1, pred.df, ~ exp(vegetation))

# gg() with sf points and geom = "tile" plots a raster
ggplot() +
  gg(int1, geom = "tile") +
  gg(boundary, alpha = 0, lwd = 2) +
  gg(nests, color = "DarkGreen")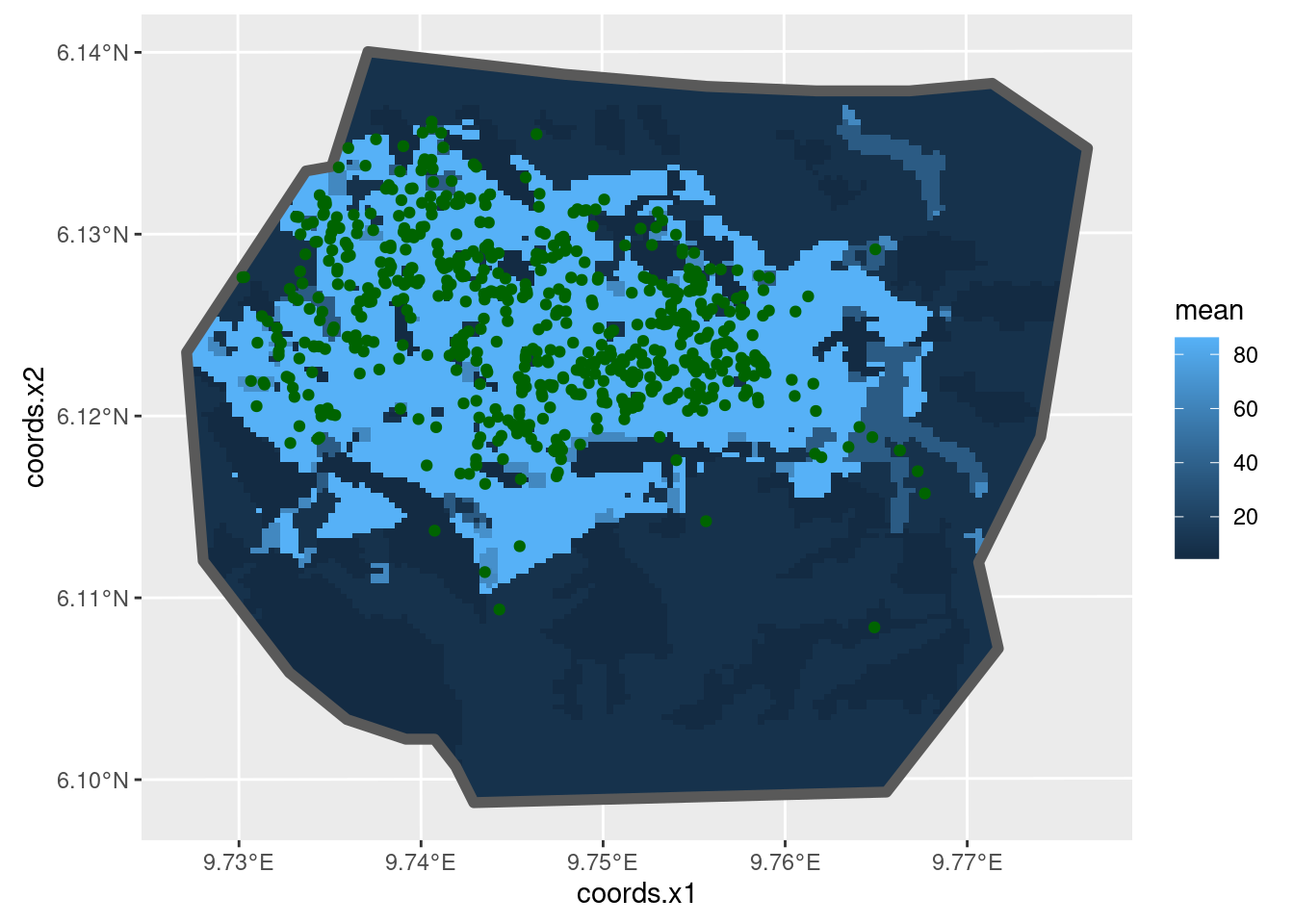

Not surprisingly, given that most nests are in Primary vegetation, the high density is in this vegetation. But there are substantial patches of predicted high density that have no nests, and some areas of predicted low density that have nests. What about the estimated abundance (there are really 647 nests there):

ips <- fm_int(mesh, boundary)
Lambda1 <- predict(fit1, ips, ~ sum(weight * exp(vegetation)))
Lambda1
#>       mean       sd   q0.025     q0.5  q0.975   median sd.mc_std_err
#> 1 647.0378 23.87926 602.8747 646.8677 690.682 646.8677      1.560915
#>   mean.mc_std_err
#> 1        2.700109

A model with vegetation type and a SPDE type smoother

Lets try to explain the pattern in nest distribution that is not captured by the vegetation covariate, using an SPDE:

pcmatern <- inla.spde2.pcmatern(mesh,
  prior.sigma = c(0.1, 0.01),
  prior.range = c(0.1, 0.01)
)

comp2 <- geometry ~
  -1 +
  vegetation(gcov$vegetation, model = "factor_full") +
  mySmooth(geometry, model = pcmatern)

fit2 <- lgcp(comp2, nests, samplers = boundary, domain = list(geometry = mesh))

And plot the posterior median intensity surface

int2 <- predict(fit2, pred.df, ~ exp(mySmooth + vegetation), n.samples = 1000)

ggplot() +
  gg(int2, aes(fill = q0.5), geom = "tile") +
  gg(boundary, alpha = 0, lwd = 2) +
  gg(nests)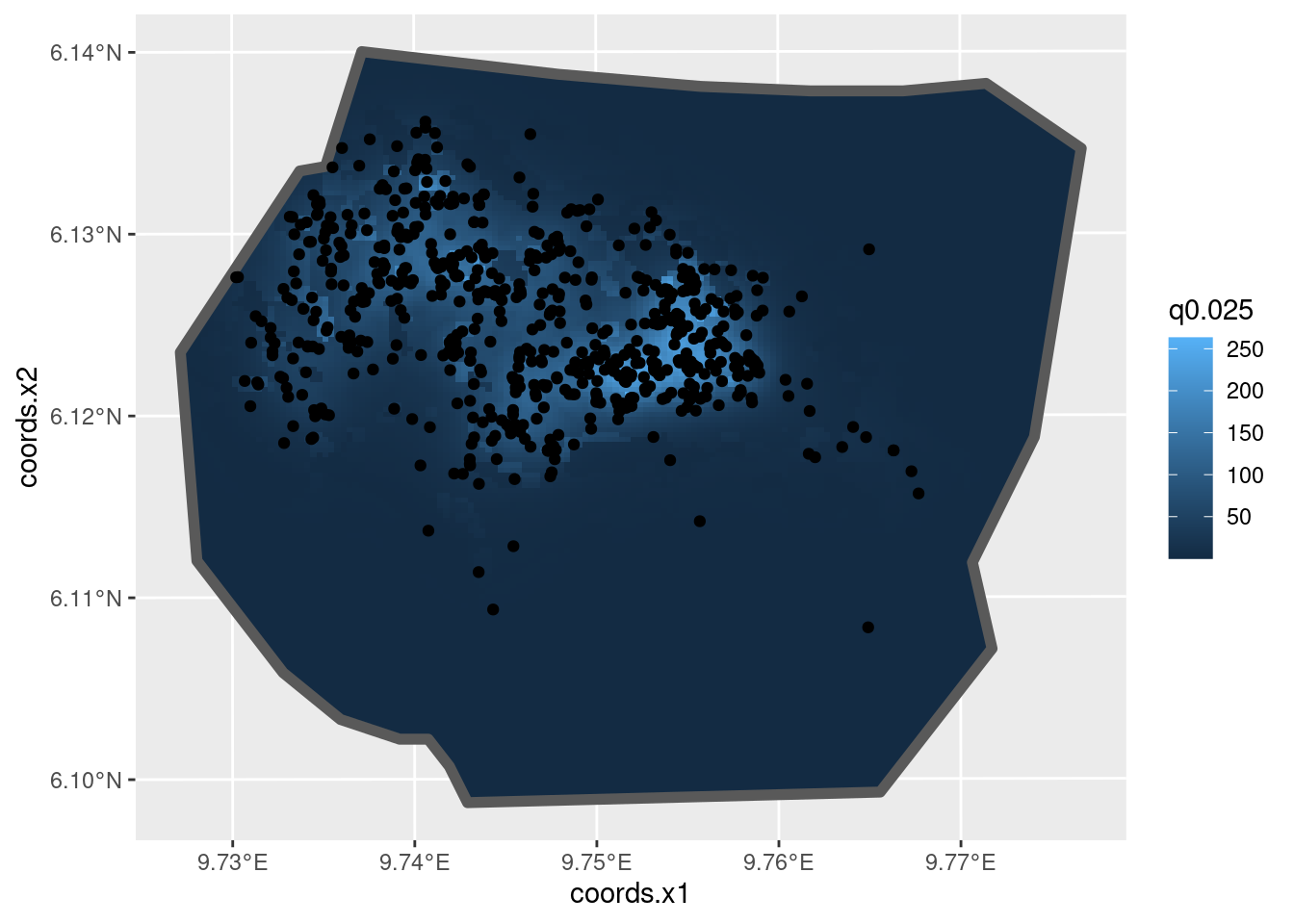

… and the expected integrated intensity (mean of abundance)

Lambda2 <- predict(
  fit2,
  fm_int(mesh, boundary),
  ~ sum(weight * exp(mySmooth + vegetation))
)
Lambda2
#>       mean       sd   q0.025     q0.5   q0.975   median sd.mc_std_err
#> 1 678.1128 28.37444 620.8096 676.3574 731.4695 676.3574      1.956762
#>   mean.mc_std_err
#> 1        3.228796

Look at the contributions to the linear predictor from the SPDE and from vegetation:

lp2 <- predict(fit2, pred.df, ~ list(
  smooth_veg = mySmooth + vegetation,
  smooth = mySmooth,
  veg = vegetation
))

The function scale_fill_gradientn sets the scale for the plot legend. Here we set it to span the range of the three linear predictor components being plotted (medians are plotted by default).

lprange <- range(lp2$smooth_veg$median, lp2$smooth$median, lp2$veg$median)
csc <- scale_fill_gradientn(colours = brewer.pal(9, "YlOrRd"), limits = lprange)

plot.lp2 <- ggplot() +
  gg(lp2$smooth_veg, geom = "tile") +
  csc +
  theme(legend.position = "bottom") +
  gg(boundary, alpha = 0) +
  ggtitle("mySmooth + vegetation")

plot.lp2.spde <- ggplot() +
  gg(lp2$smooth, geom = "tile") +
  csc +
  theme(legend.position = "bottom") +
  gg(boundary, alpha = 0) +
  ggtitle("mySmooth")

plot.lp2.veg <- ggplot() +
  gg(lp2$veg, geom = "tile") +
  csc +
  theme(legend.position = "bottom") +
  gg(boundary, alpha = 0) +
  ggtitle("vegetation")

multiplot(plot.lp2, plot.lp2.spde, plot.lp2.veg, cols = 3)

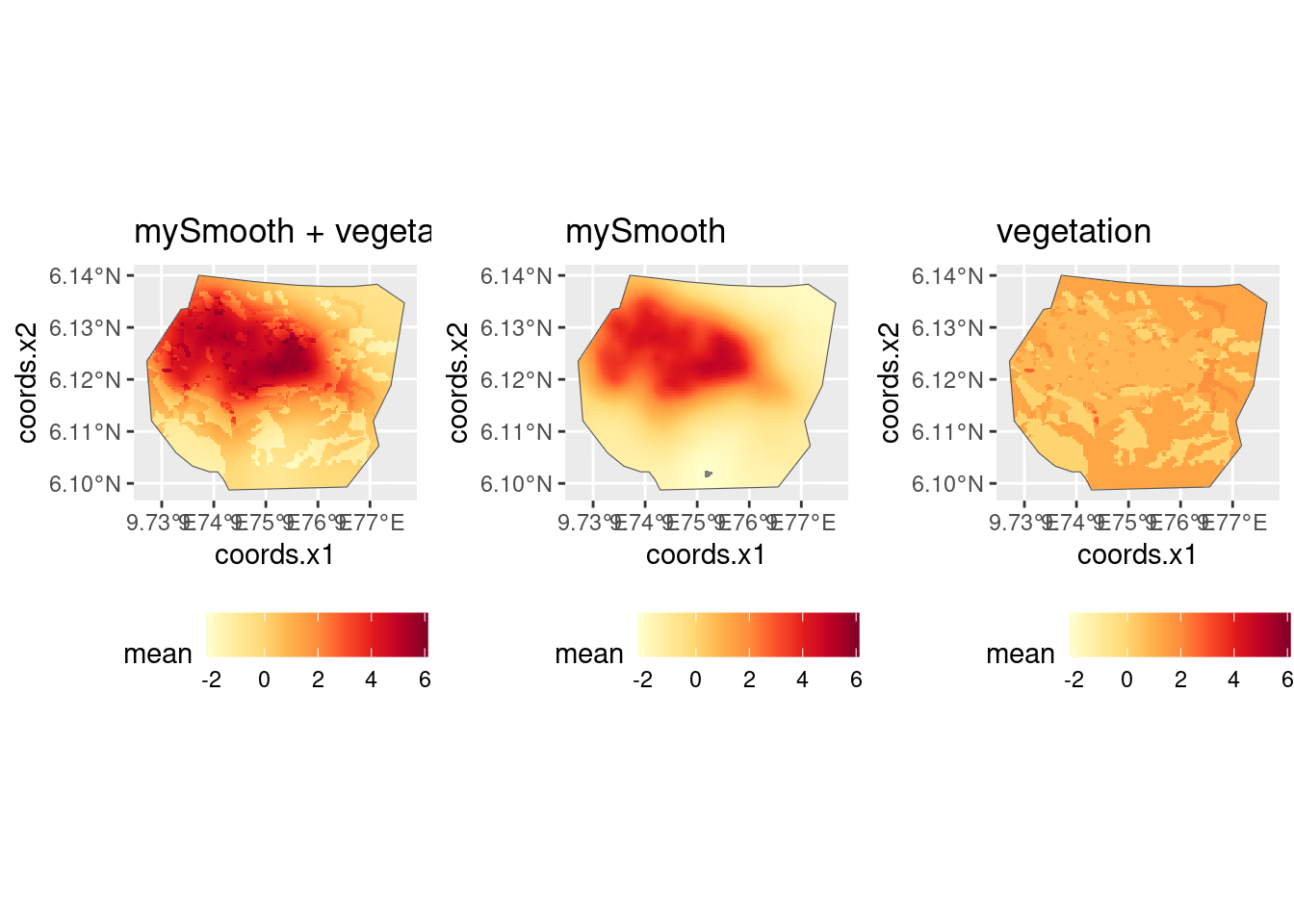
A model with SPDE only

Do we need vegetation at all? Fit a model with only an SPDE + Intercept, and choose between models on the basis of DIC, using deltaIC().

comp3 <- geometry ~ mySmooth(geometry, model = pcmatern) + Intercept(1)
fit3 <- lgcp(comp3,
  data = nests,
  samplers = boundary,
  domain = list(geometry = mesh)
)

int3 <- predict(fit3, pred.df, ~ exp(mySmooth + Intercept))

ggplot() +
  gg(int3, geom = "tile") +
  gg(boundary, alpha = 0) +
  gg(nests)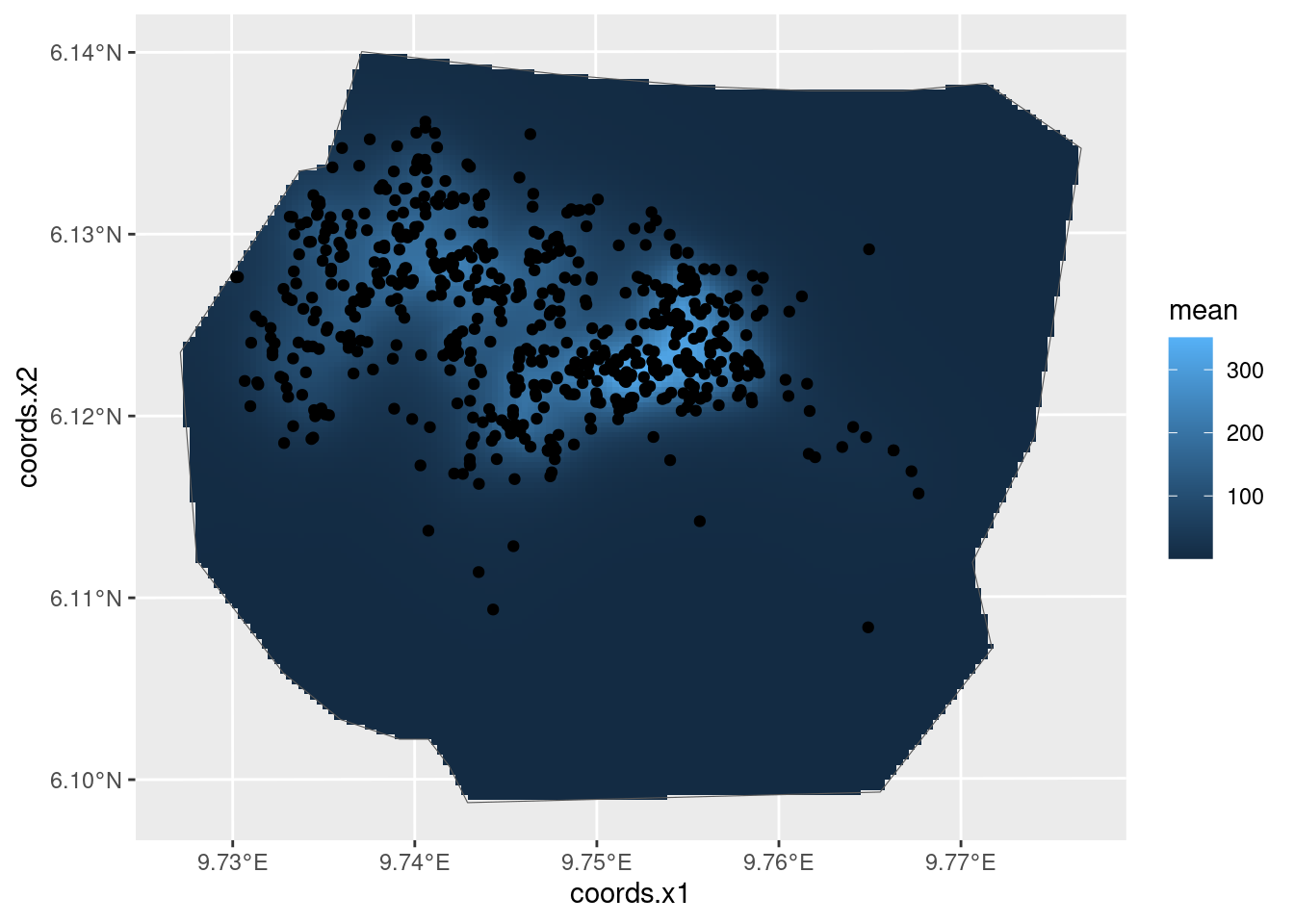

Lambda3 <- predict(
  fit3,
  fm_int(mesh, boundary),
  ~ sum(weight * exp(mySmooth + Intercept))
)
Lambda3
#>       mean       sd   q0.025     q0.5   q0.975   median sd.mc_std_err
#> 1 677.3011 29.28016 626.6763 673.5165 731.4265 673.5165      1.940932
#>   mean.mc_std_err
#> 1        3.316203

knitr::kable(deltaIC(fit1, fit2, fit3, criterion = c("DIC")))

Model	DIC	Delta.DIC
fit1	-562.5418	0.000
fit3	524.8545	1087.396
fit2	619.0922	1181.634

NOTE: the behaviour of DIC is currently a bit unclear, and is being investigated. WAIC is related to leave-one-out cross-validation, and is not appropriate to use with the current current LGCP likelihood implementation.

Classic mode:

Model	DIC	Delta.DIC
fit2	2224.131	0.00000
fit3	2274.306	50.17504
fit1	3124.784	900.65339

Experimental mode:

Model	DIC	Delta.DIC
fit1	-563.3583	0.000
fit3	509.4010	1072.759
fit2	597.6459	1161.004

CV and SPDE parameters for Model 2

We are going with Model fit2. Lets look at the spatial distribution of the coefficient of variation

ggplot() +
  gg(int2, aes(fill = sd / mean), geom = "tile") +
  gg(boundary, alpha = 0) +
  gg(nests)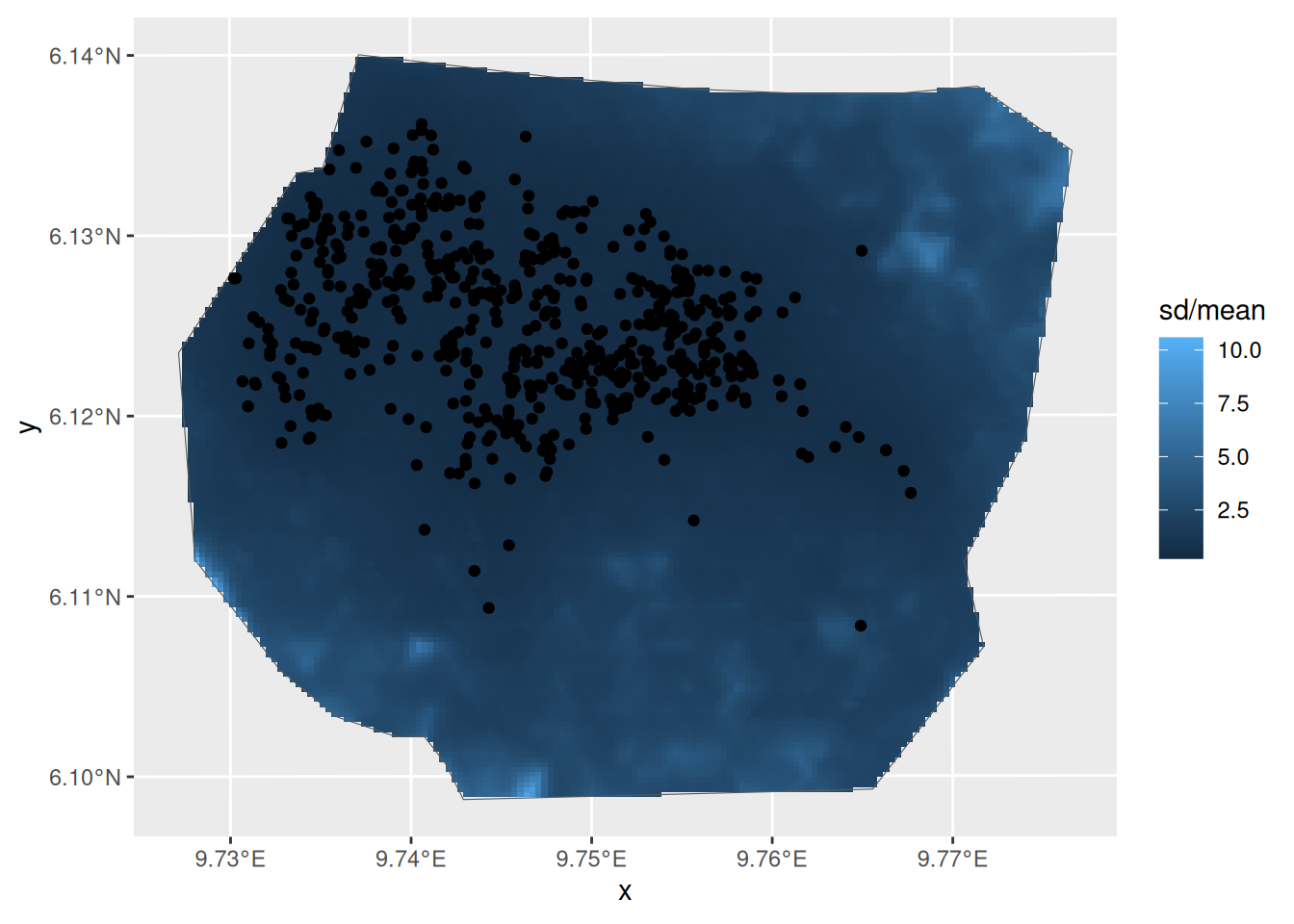

Plot the vegetation “fixed effect” posteriors. First get their names - from $marginals.random$vegetation of the fitted object, which contains the fixed effect marginal distribution data

flist <- vector("list", NROW(fit2$summary.random$vegetation))
for (i in seq_along(flist)) flist[[i]] <- plot(fit2, "vegetation", index = i)
multiplot(plotlist = flist, cols = 3)

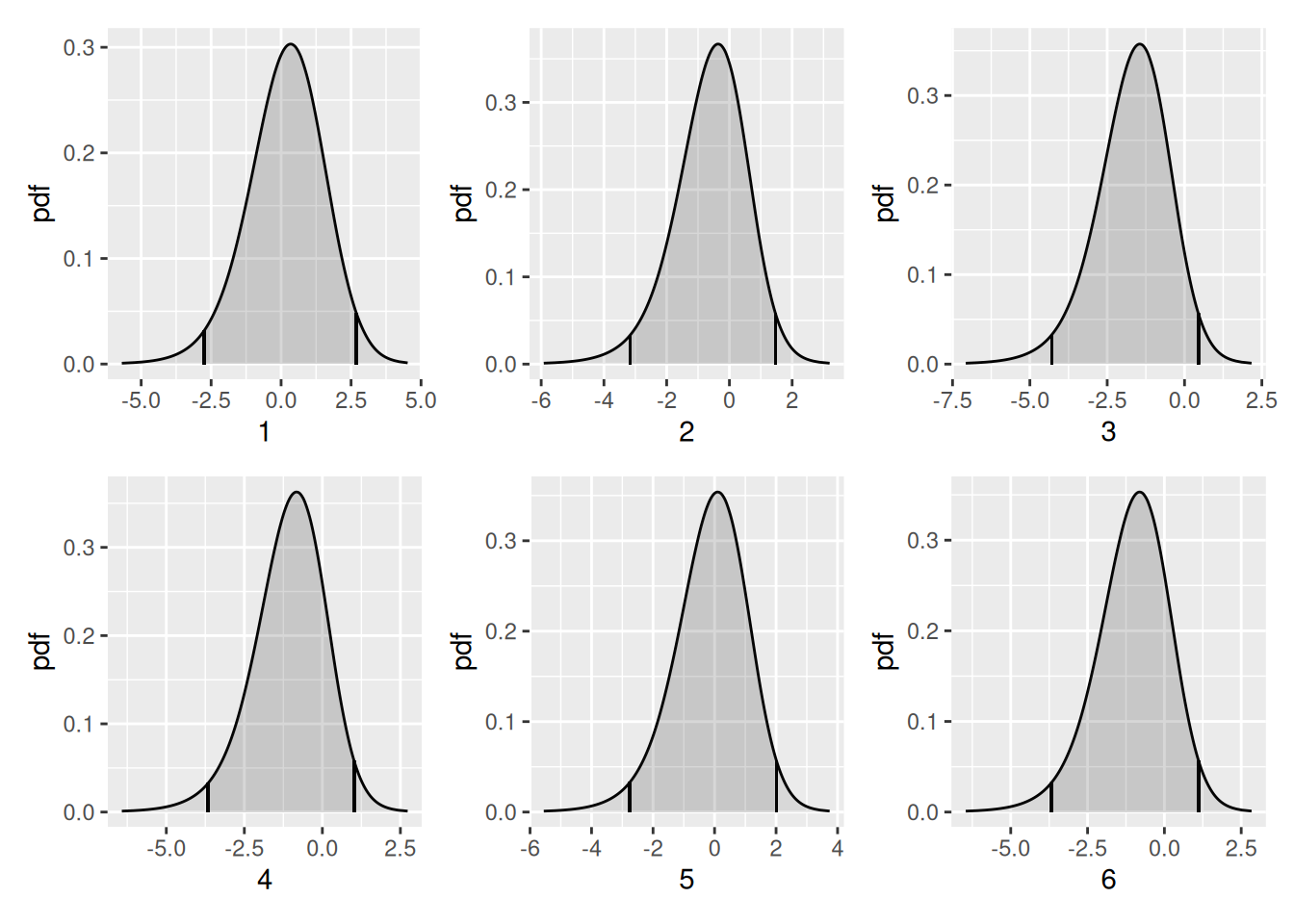
Use spde.posterior( ) to obtain and then plot the SPDE parameter posteriors and the Matern correlation and covariance functions for this model.

spde.range <- spde.posterior(fit2, "mySmooth", what = "range")
spde.logvar <- spde.posterior(fit2, "mySmooth", what = "log.variance")
range.plot <- plot(spde.range)
var.plot <- plot(spde.logvar)

multiplot(range.plot, var.plot)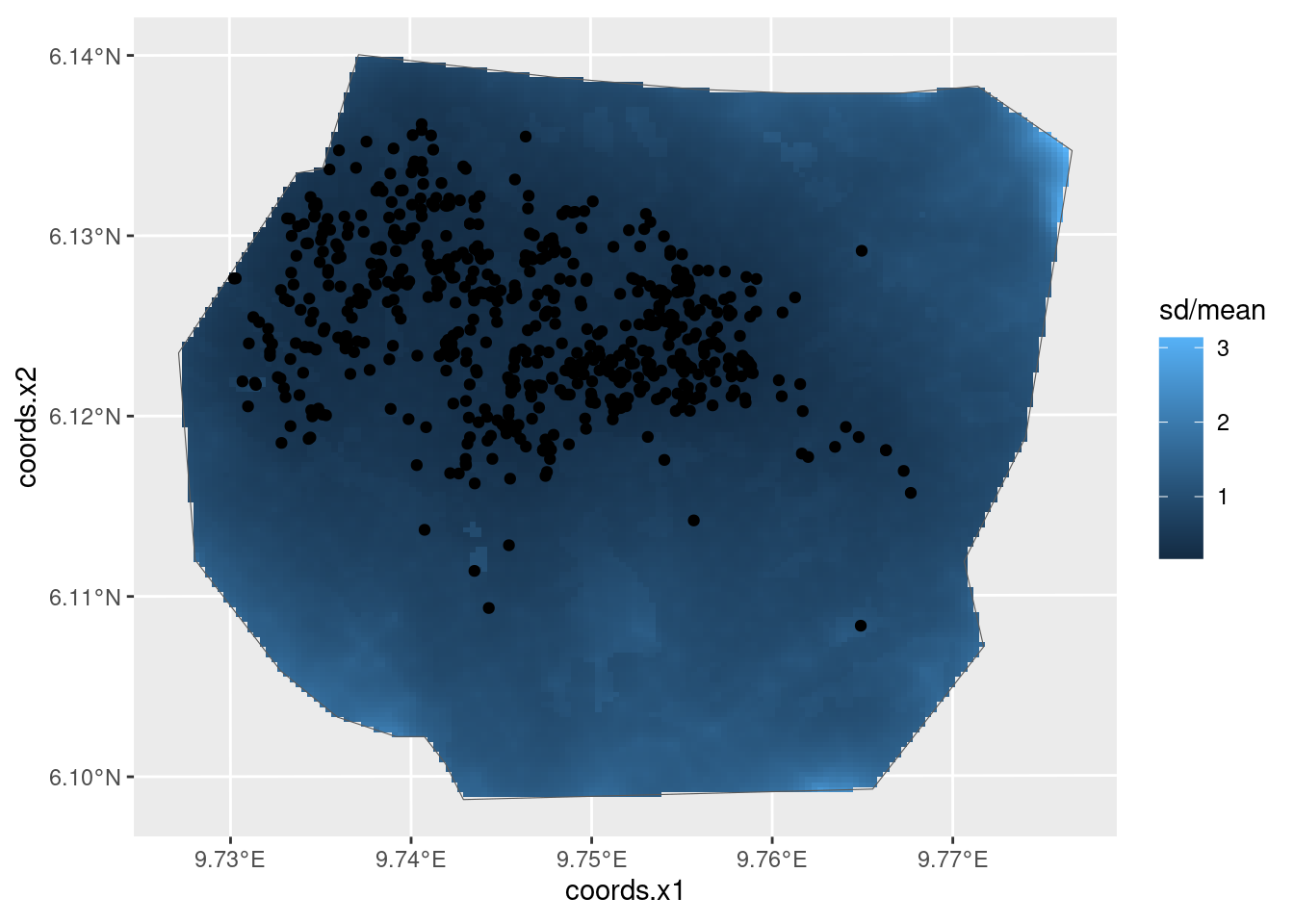

corplot <- plot(spde.posterior(fit2, "mySmooth", what = "matern.correlation"))
covplot <- plot(spde.posterior(fit2, "mySmooth", what = "matern.covariance"))
multiplot(covplot, corplot)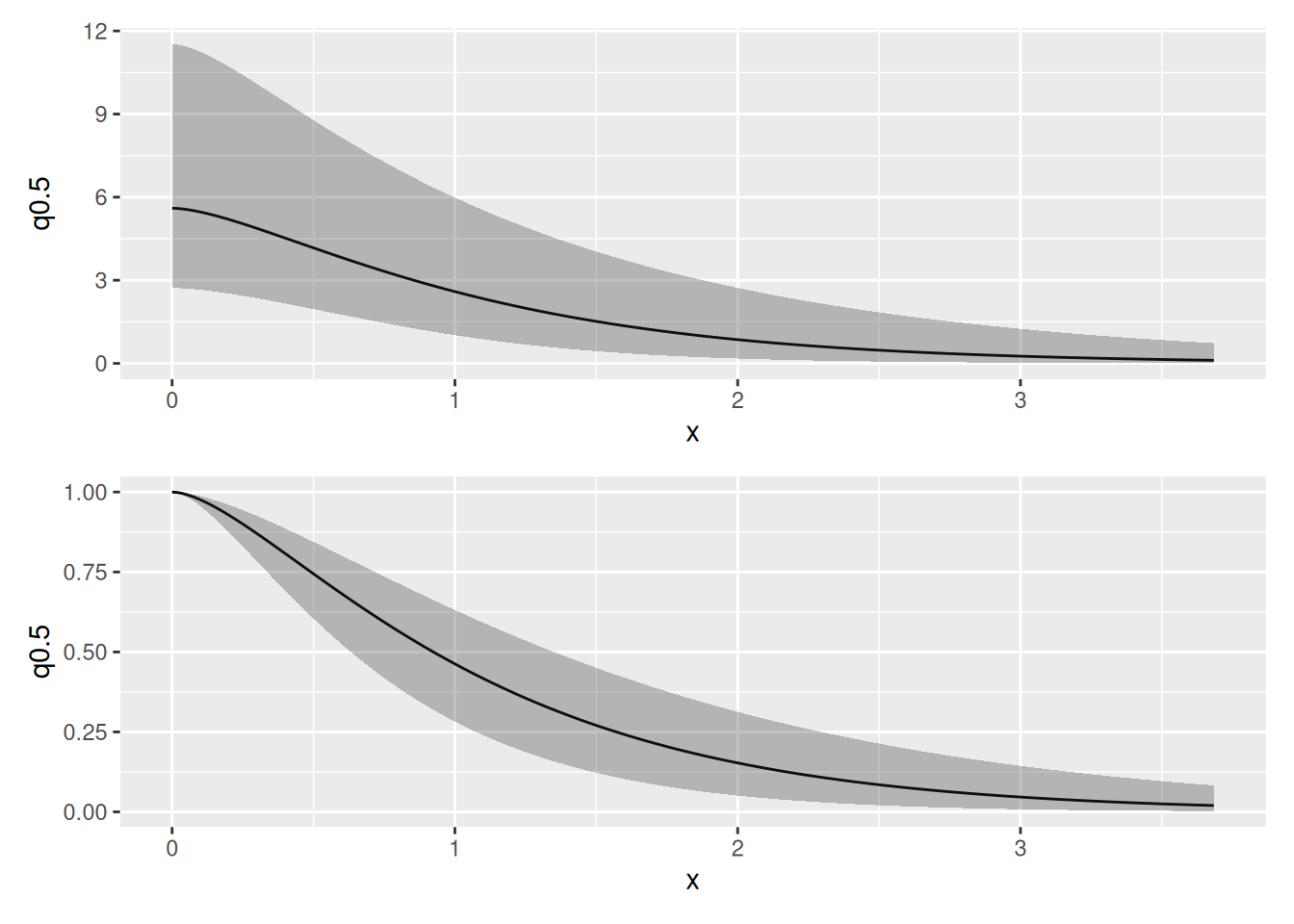

Continuous covariates

Now lets try a model with elevation as a (continuous) explanatory variable. (First centre elevations for more stable fitting.)

elev <- gcov$elevation
elev <- elev - mean(terra::values(elev), na.rm = TRUE)

ggplot() +
  gg(elev, geom = "tile") +
  gg(boundary, alpha = 0)

The elevation variable here is of class ‘SpatRaster’, that can be handled in the same way as the vegetation covariate, with automatic evaluation via an eval_spatial() method. However, since in some cases data may be stored differently, other methods are needed to access the stored values, or there’s some post-processing to be done. In such cases, we can define a function that knows how to evaluate the covariate at arbitrary points in the survey region, and call that function in the component definition. The method eval_spatial() is the method that handles this automatically, and supports terra SpatRaster and sf geometry points objects, and mismatching coordinate systems as well. In the following evaluator example function, we only add infilling of missing values as a post-processing step.

# Note: this method is usually not needed; the automatic invocation of
# `eval_spatial()` method by the component input evaluator is usually
# sufficient.
f.elev <- function(where) {
  # Extract the values
  v <- eval_spatial(elev, where, layer = "elevation")
  # Fill in missing values; this example would work for
  # SpatialPixelsDataFrame data
  # if (any(is.na(v))) {
  #   v <- bru_fill_missing(elev, where, v)
  # }
  v
}

For brevity we are not going to consider models with elevation only, with elevation and a SPDE, and with SPDE only. We will just fit one with elevation and SPDE. We create our model to pass to lgcp thus:

matern <- inla.spde2.pcmatern(mesh,
  prior.sigma = c(0.1, 0.01),
  prior.range = c(0.1, 0.01)
)

ecomp <- geometry ~ elev(f.elev(.data.), model = "linear") +
  mySmooth(geometry, model = matern) + Intercept(1)

Note how the elevation effect is defined. We could alternatively use the terra grid object directly (causing inlabru to automatically call eval_spatial()), like in the vegetation case: we specified it like

elev(elev, model = "factor_full")

whereas with the special function method we specify the covariate like this:

elev(f.elev(.data.), model = "linear")

Most applications can use the automatic method, and the special function method is included only as an example of how to handle more complex cases.

We also now include an intercept term in the model.

The model is fitted in the usual way:

efit <- lgcp(ecomp, nests, samplers = boundary, domain = list(geometry = mesh))

Summary and model selection

summary(efit)
#> inlabru version: 2.12.0.9015
#> INLA version: 25.05.04-1
#> Components:
#> elev: main = linear(f.elev(.data.)), group = exchangeable(1L), replicate = iid(1L), NULL
#> mySmooth: main = spde(geometry), group = exchangeable(1L), replicate = iid(1L), NULL
#> Intercept: main = linear(1), group = exchangeable(1L), replicate = iid(1L), NULL
#> Observation models:
#>   Family: 'cp'
#>     Tag: ''
#>     Data class: 'sf', 'data.frame'
#>     Response class: 'numeric'
#>     Predictor: geometry ~ .
#>     Additive/Linear: TRUE/TRUE
#>     Used components: effects[elev, mySmooth, Intercept], latent[]
#> Time used:
#>     Pre = 0.359, Running = 13.1, Post = 0.359, Total = 13.8 
#> Fixed effects:
#>            mean    sd 0.025quant 0.5quant 0.975quant  mode kld
#> elev      0.004 0.001      0.002    0.004      0.006 0.004   0
#> Intercept 1.126 0.478      0.152    1.137      2.038 1.137   0
#> 
#> Random effects:
#>   Name     Model
#>     mySmooth SPDE2 model
#> 
#> Model hyperparameters:
#>                    mean    sd 0.025quant 0.5quant 0.975quant  mode
#> Range for mySmooth 1.76 0.217      1.376     1.74       2.23 1.712
#> Stdev for mySmooth 1.00 0.085      0.847     1.00       1.18 0.996
#> 
#> Deviance Information Criterion (DIC) ...............: 521.17
#> Deviance Information Criterion (DIC, saturated) ....: 520.35
#> Effective number of parameters .....................: -825.31
#> 
#> Watanabe-Akaike information criterion (WAIC) ...: 1604.12
#> Effective number of parameters .................: 153.73
#> 
#> Marginal log-Likelihood:  -1254.95 
#>  is computed 
#> Posterior summaries for the linear predictor and the fitted values are computed
#> (Posterior marginals needs also 'control.compute=list(return.marginals.predictor=TRUE)')
deltaIC(fit1, fit2, fit3, efit)
#>   Model       DIC Delta.DIC
#> 1  fit1 -562.5418     0.000
#> 2  efit  521.1749  1083.717
#> 3  fit3  524.8545  1087.396
#> 4  fit2  619.0922  1181.634

Predict and plot the density

e.pred <- predict(
  efit,
  pred.df,
  ~ list(
    int = exp(mySmooth + elev + Intercept),
    int.log = mySmooth + elev + Intercept
  )
)

p1 <- ggplot() +
  gg(e.pred$int, aes(fill = log(sd)), geom = "tile") +
  gg(boundary, alpha = 0) +
  gg(nests, shape = "+")
p2 <- ggplot() +
  gg(e.pred$int.log, aes(fill = exp(mean + sd^2 / 2)), geom = "tile") +
  gg(boundary, alpha = 0) +
  gg(nests, shape = "+")
library(patchwork)
p1 | p2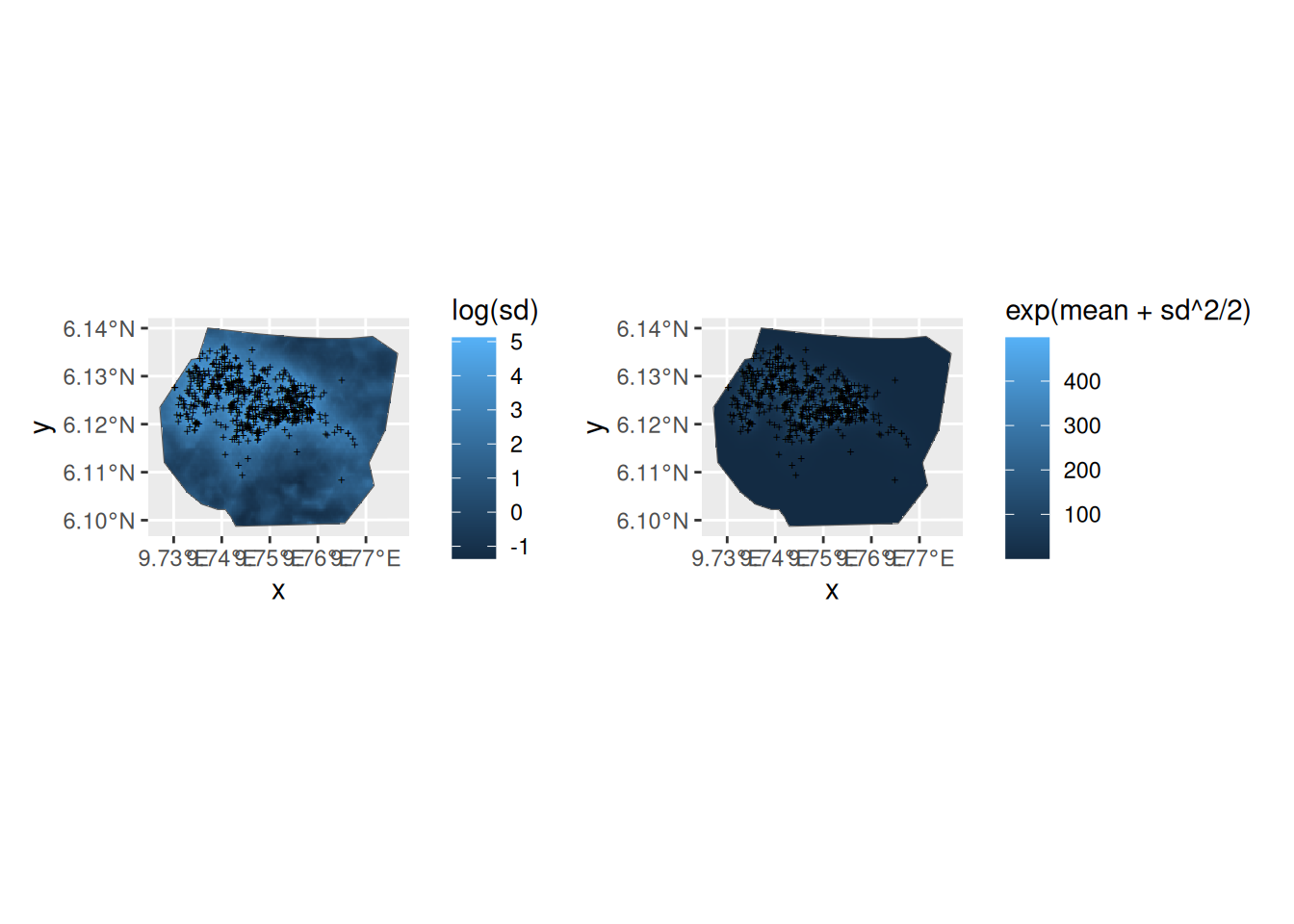

Now look at the elevation and SPDE effects in space. Leave out the Intercept because it swamps the spatial effects of elevation and the SPDE in the plots and we are interested in comparing the effects of elevation and the SPDE.

First we need to predict on the linear predictor scale.

e.lp <- predict(
  efit,
  pred.df,
  ~ list(
    smooth_elev = mySmooth + elev,
    elev = elev,
    smooth = mySmooth
  )
)

The code below, which is very similar to that used for the vegetation factor variable, produces the plots we want.

lprange <- range(e.lp$smooth_elev$mean, e.lp$elev$mean, e.lp$smooth$mean)

library(RColorBrewer)
csc <- scale_fill_gradientn(colours = brewer.pal(9, "YlOrRd"), limits = lprange)

plot.e.lp <- ggplot() +
  gg(e.lp$smooth_elev, mask = boundary, geom = "tile") +
  csc +
  theme(legend.position = "bottom") +
  gg(boundary, alpha = 0) +
  ggtitle("SPDE + elevation")

plot.e.lp.spde <- ggplot() +
  gg(e.lp$smooth, mask = boundary, geom = "tile") +
  csc +
  theme(legend.position = "bottom") +
  gg(boundary, alpha = 0) +
  ggtitle("SPDE")

plot.e.lp.elev <- ggplot() +
  gg(e.lp$elev, mask = boundary, geom = "tile") +
  csc +
  theme(legend.position = "bottom") +
  gg(boundary, alpha = 0) +
  ggtitle("elevation")

multiplot(plot.e.lp,
  plot.e.lp.spde,
  plot.e.lp.elev,
  cols = 3
)

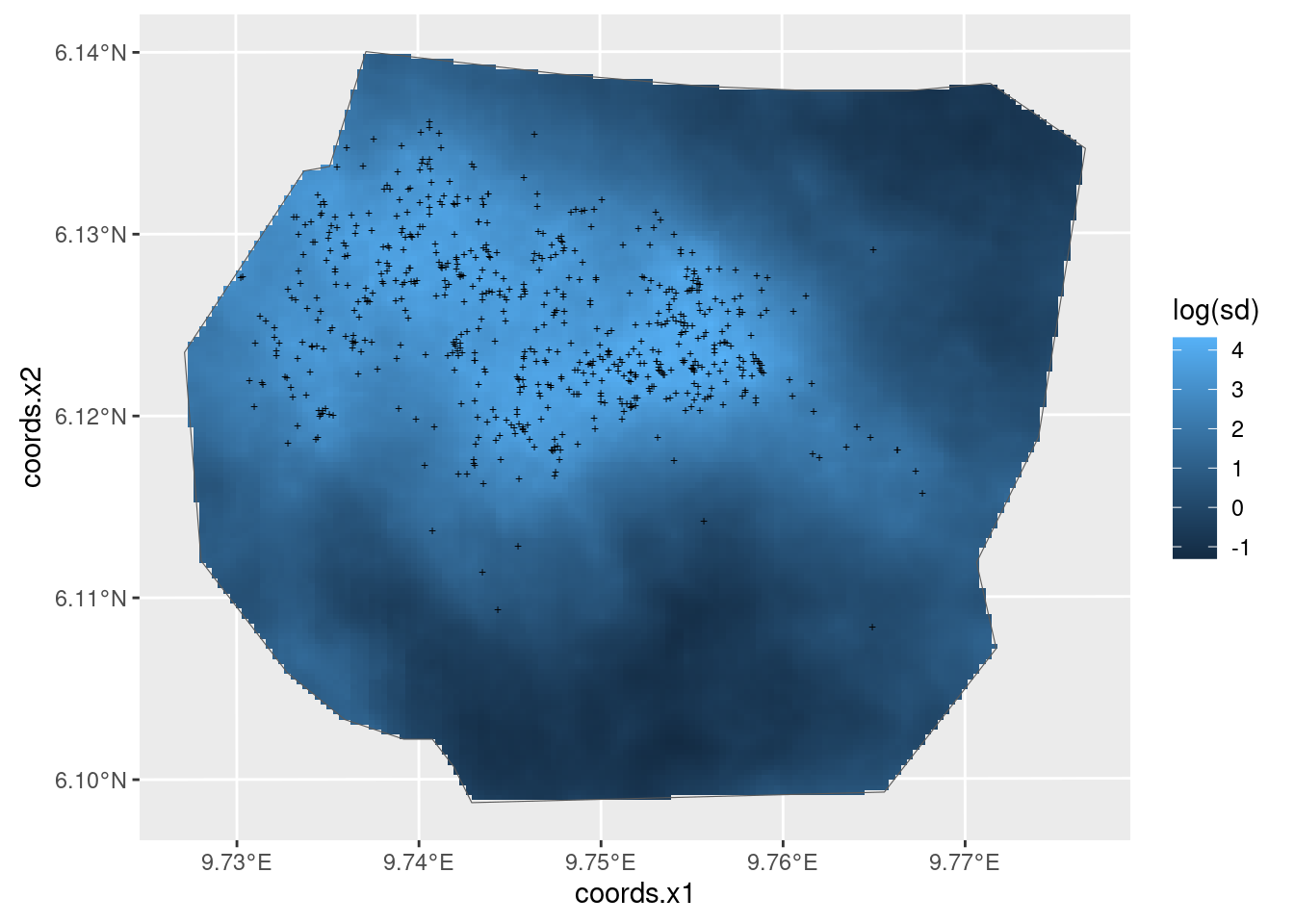
You might also want to look at the posteriors of the fixed effects and of the SPDE. Adapt the code used for the vegetation factor to do this.

LambdaE <- predict(
  efit,
  fm_int(mesh, boundary),
  ~ sum(weight * exp(Intercept + elev + mySmooth))
)
LambdaE
#>       mean       sd   q0.025     q0.5   q0.975   median sd.mc_std_err
#> 1 670.5155 27.76786 616.2393 669.0375 728.4672 669.0375      2.090693
#>   mean.mc_std_err
#> 1        3.194925

flist <- vector("list", NROW(efit$summary.fixed))
for (i in seq_along(flist)) {
  flist[[i]] <- plot(efit, rownames(efit$summary.fixed)[i])
}
multiplot(plotlist = flist, cols = 2)

Plot the SPDE parameter posteriors and the Matern correlation and covariance functions for this model.

spde.range <- spde.posterior(efit, "mySmooth", what = "range")
spde.logvar <- spde.posterior(efit, "mySmooth", what = "log.variance")
range.plot <- plot(spde.range)
var.plot <- plot(spde.logvar)

multiplot(range.plot, var.plot)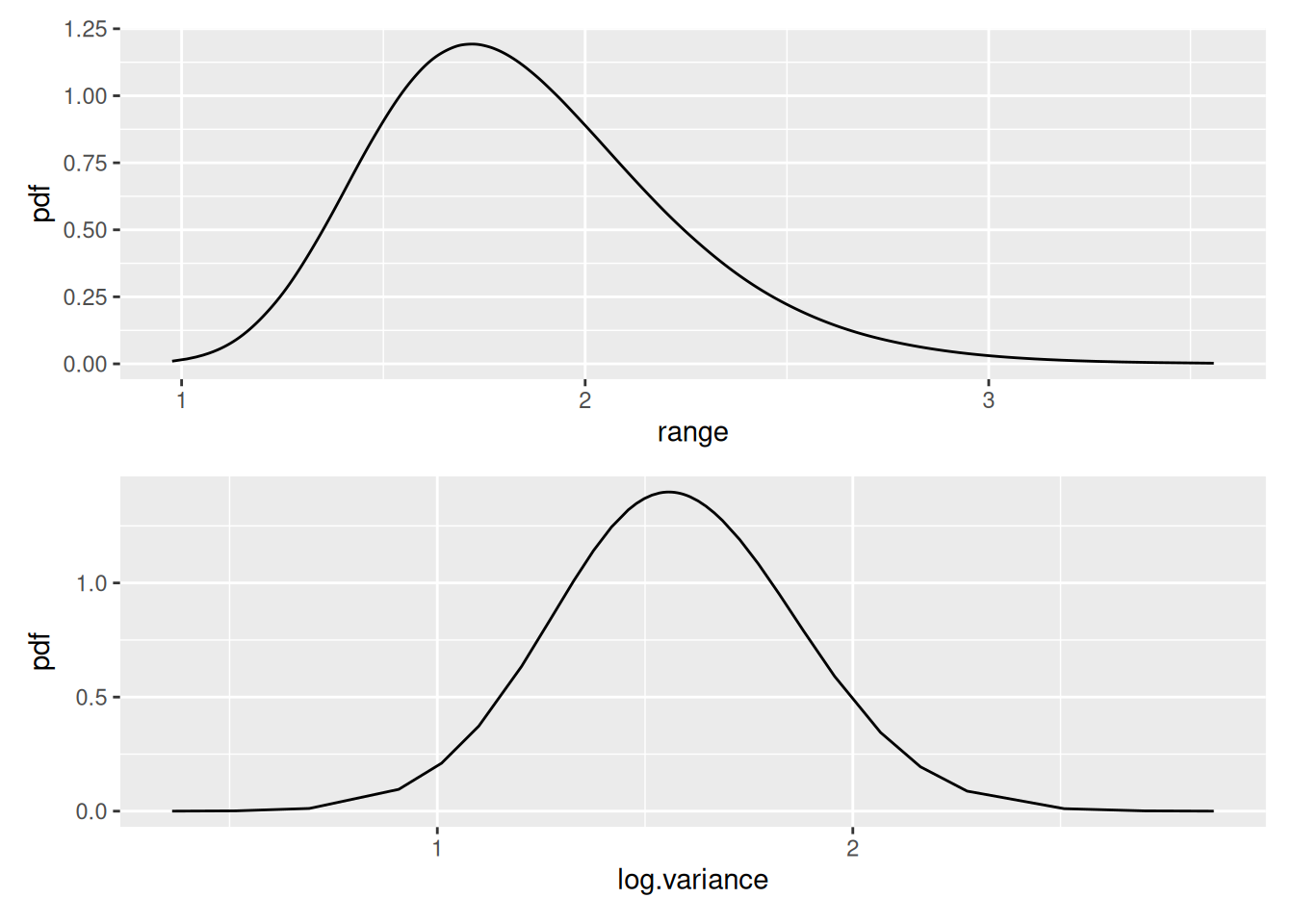

corplot <- plot(spde.posterior(efit, "mySmooth", what = "matern.correlation"))
covplot <- plot(spde.posterior(efit, "mySmooth", what = "matern.covariance"))
multiplot(covplot, corplot)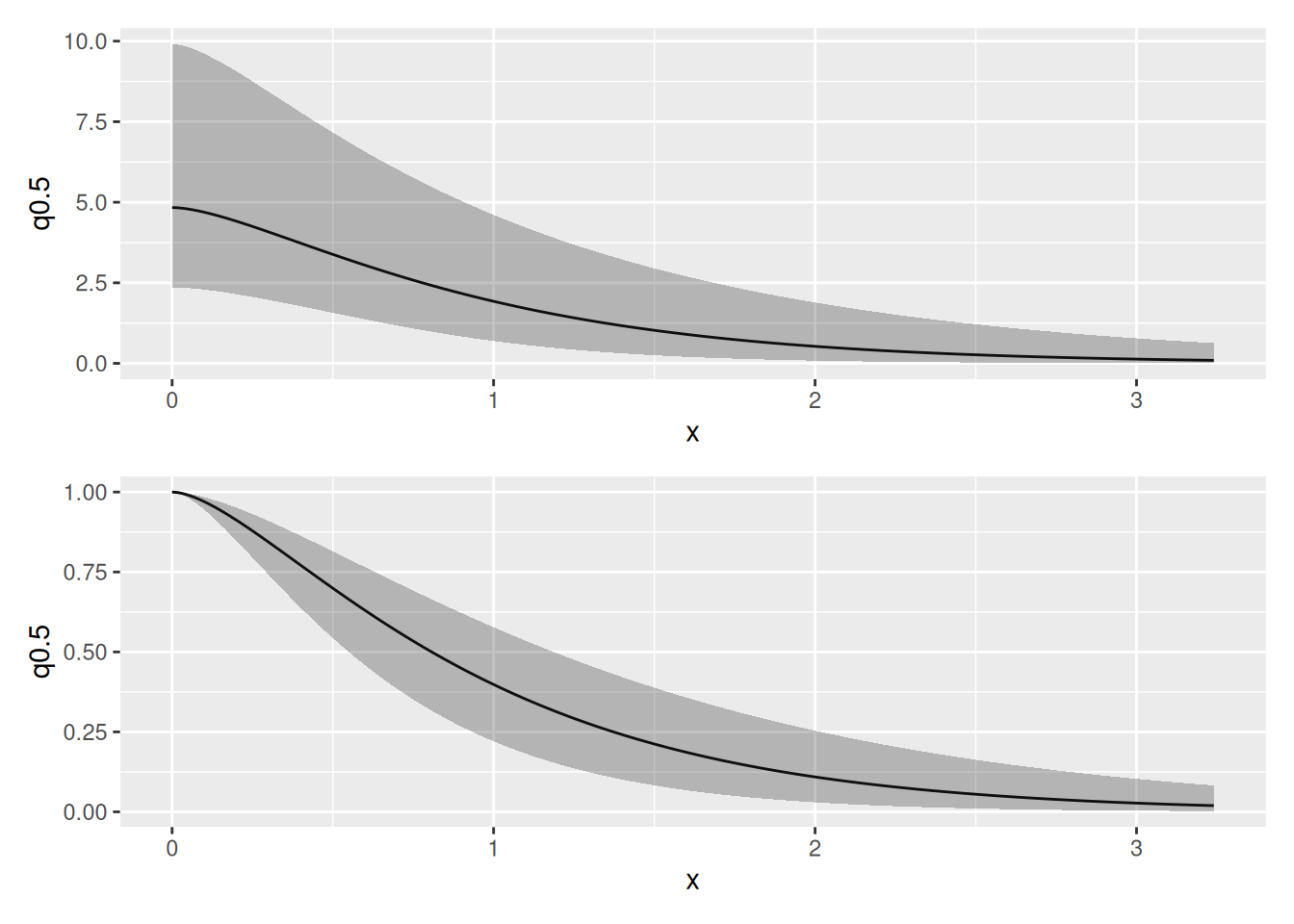

Also estimate abundance. The data.frame in the second call leads to inclusion of N in the prediction object, for easier plotting.

Lambda <- predict(
  efit, fm_int(mesh, boundary),
  ~ sum(weight * exp(mySmooth + elev + Intercept))
)
Lambda
#>       mean       sd   q0.025     q0.5   q0.975   median sd.mc_std_err
#> 1 675.8898 27.49661 630.7317 677.9338 734.8247 677.9338      2.192179
#>   mean.mc_std_err
#> 1        3.188097

Nest.e <- predict(
  efit,
  fm_int(mesh, boundary),
  ~ data.frame(
    N = 200:1000,
    density = dpois(200:1000,
      lambda = sum(weight * exp(mySmooth + elev + Intercept))
    )
  ),
  n.samples = 2000
)

Plot in the same way as in previous practicals

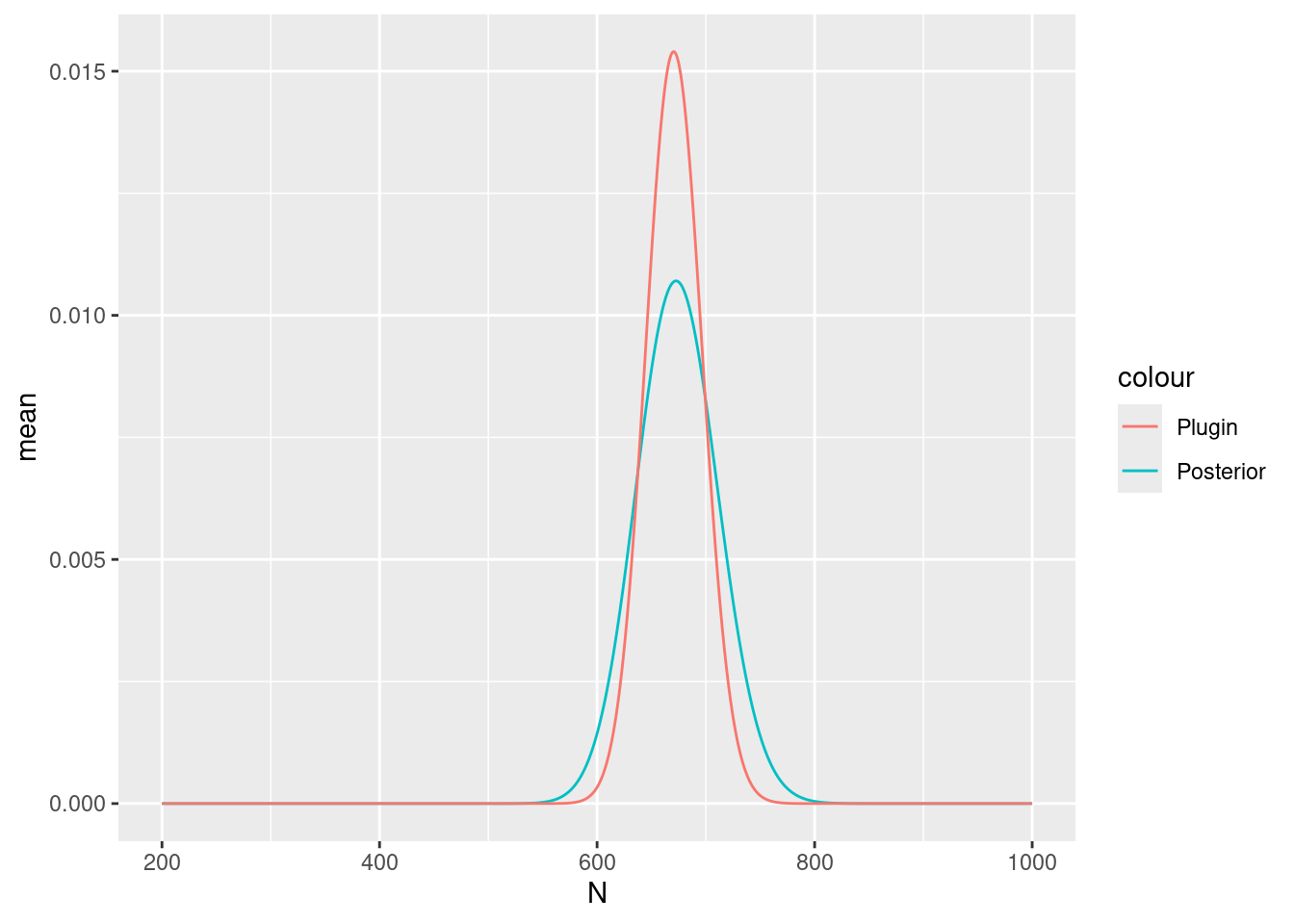
Nest.e$plugin_estimate <- dpois(Nest.e$N, lambda = Lambda$median)
ggplot(data = Nest.e) +
  geom_line(aes(x = N, y = mean, colour = "Posterior")) +
  geom_line(aes(x = N, y = plugin_estimate, colour = "Plugin"))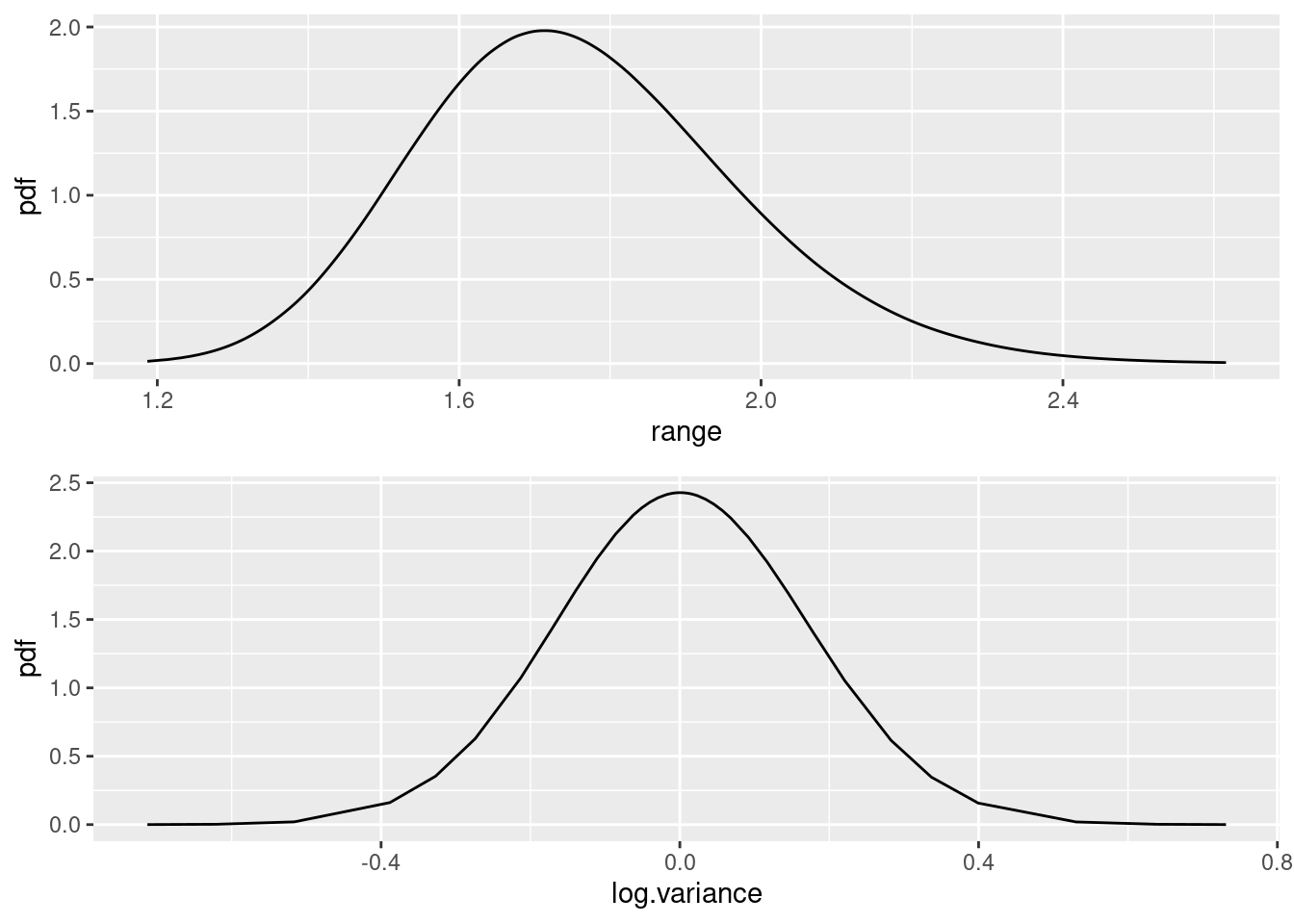

Non-spatial evaluation of the covariate effect

The previous examples of posterior prediction focused on spatial prediction. It is also possible to evaluate the effect of a covariate directly, by bypassing the component definition input. This is done by adding the suffix _eval() to the end of the component name in the predictor expression, and supplying data that is sufficient for evaluating , and supplying data needed by the input arguments to this function, see bru_component_eval().

Note on backwards version support, starting with version 2.2.8 Prior to version 2.8.0, this feature required setting the include argument to character(0) to disable normal component evaluation for all components. From version 2.8.0, inlabru automatically detects which model components are used by the prediction expression, including the use of component _eval() calls, making the include argument unnecessary. From version 2.11.0, the include, exclude, and include_latent arguments have been deprecated in favour of the used argument that takes input generated by bru_used(), with a deprecation warning being generated from version 2.12.0.9003.

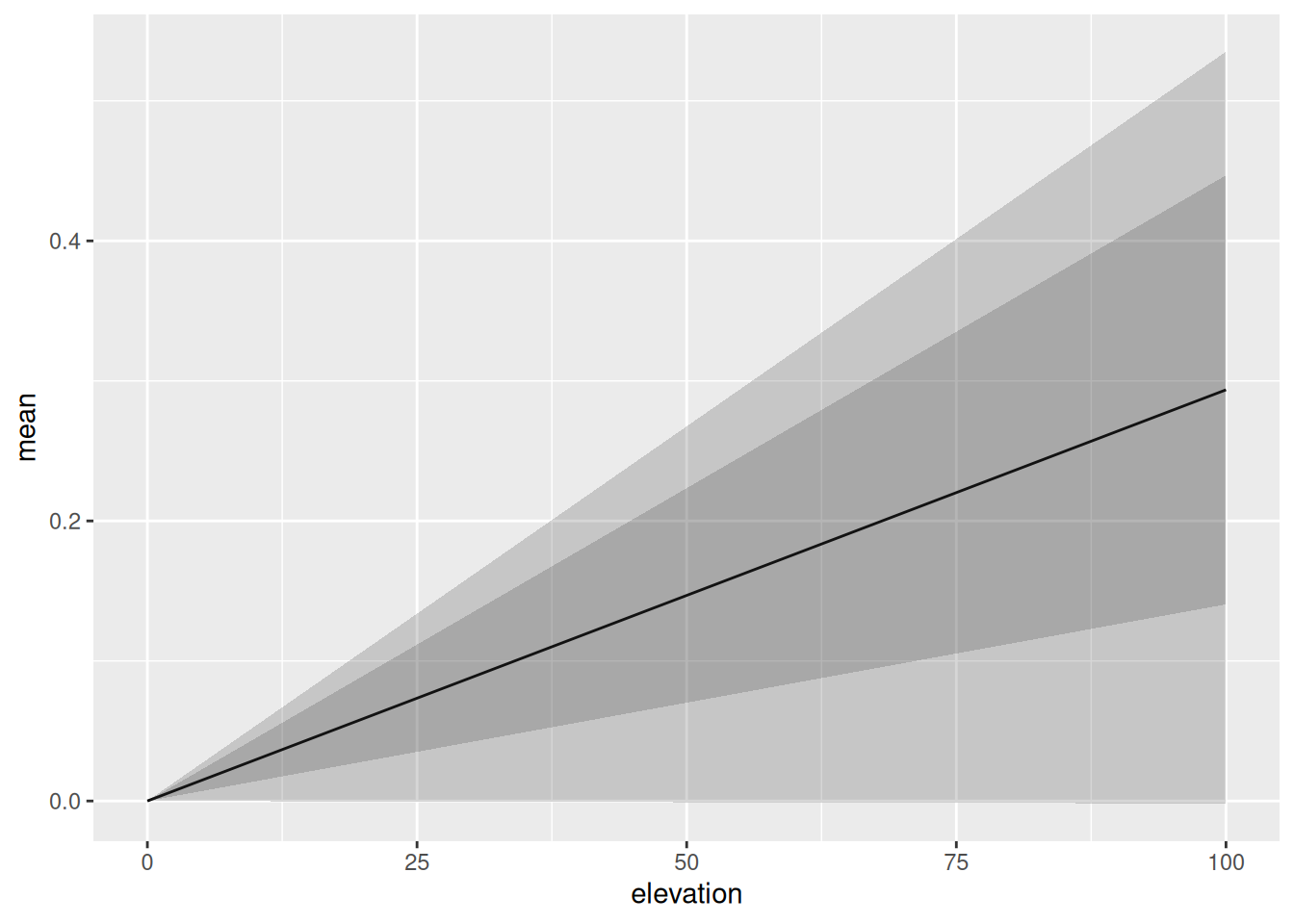
Since the elevation effect in this model is linear, the resulting plot isn’t very interesting, but the same method can be applied to non-linear effects (e.g. “rw2”) as well, and combined into general R expressions.

elev.pred <- predict(
  efit,
  data.frame(elevation = seq(0, 100, length.out = 1000)),
  formula = ~ elev_eval(elevation)
  # include = character(0) # Not needed from version 2.8.0
)

ggplot(elev.pred) +
  geom_line(aes(elevation, mean)) +
  geom_ribbon(
    aes(elevation,
      ymin = q0.025,
      ymax = q0.975
    ),
    alpha = 0.2
  ) +
  geom_ribbon(
    aes(elevation,
      ymin = mean - 1 * sd,
      ymax = mean + 1 * sd
    ),
    alpha = 0.2
  )

A 1D Example

Try fitting a 1-dimensional model to the point data in the inlabru dataset Poisson2_1D. This comes with a covariate function called cov2_1D. Try to reproduce the plot below (used in lectures) showing the effects of the Intercept + z and the SPDE. (You may find it helpful to build on the model you fitted in the previous practical, adding the covariate to the model specification.)

data(Poisson2_1D)
x <- seq(0, 55, length.out = 50)
mesh <- fm_mesh_1d(x, degree = 2, boundary = "free")

process_model <- inla.spde2.pcmatern(
  mesh,
  prior.sigma = c(1, 0.01),
  prior.range = c(5, 0.01),
  constr = TRUE
)
comp <- x ~
  z(cov2_1D(x), model = "linear") +
  smooth(x, model = process_model) +
  Intercept(1)

fitcov1D <- lgcp(comp,
  pts2,
  domain = list(x = mesh),
  samplers = tibble::tibble(x = cbind(0, 55))
)
pr.df <- data.frame(x = x)
prcov1D <- predict(
  fitcov1D,
  pr.df,
  ~ list(
    Intensity = exp(z + smooth + Intercept),
    z = exp(z + Intercept),
    smooth = exp(smooth)
  ),
  n.samples = 2000
)

ggplot() +
  gg(prcov1D$Intensity,
    aes(colour = "Intensity", fill = "Intensity"),
    alpha = 0.2,
    lwd = 1.25
  ) +
  gg(prcov1D$smooth,
    aes(colour = "Smooth", fill = "Smooth"),
    alpha = 0.2,
    lwd = 1.25
  ) +
  gg(prcov1D$z,
    aes(colour = "z-effect", fill = "z-effect"),
    alpha = 0.2,
    lwd = 1.25
  ) +
  geom_line(aes(x, lambda2_1D(x), colour = "True intensity"), lwd = 1.25) +
  geom_point(data = pts2, aes(x = x), y = 0.2, shape = "|", cex = 4) +
  xlab(quote(bold(s))) +
  ylab(quote(hat(lambda)(bold(s)) ~ ~"and its components")) +
  guides(colour = guide_legend("Quantity"), fill = "none")

LGCPs - Spatial covariates

David Borchers and Finn Lindgren

Generated on 2025-05-05