LGCPs - An example in one dimension • inlabru

Introduction

In this vignette we are going to see how to fit an SPDE to one-dimensional point data, i.e. data that consist of the points at which things are located, not the number of points in some area.

Setting things up

Load libraries

library(inlabru)
library(INLA)
library(mgcv)
library(ggplot2)
library(fmesher)

Get the data

data(Poisson2_1D, package = "inlabru")

Take a look at the point (and frequency) data

ggplot(pts2) +
  geom_histogram(aes(x = x),
    binwidth = 55 / 20,
    boundary = 0, fill = NA, color = "black"
  ) +
  geom_point(aes(x), y = 0, pch = "|", cex = 4) +
  coord_fixed(ratio = 1)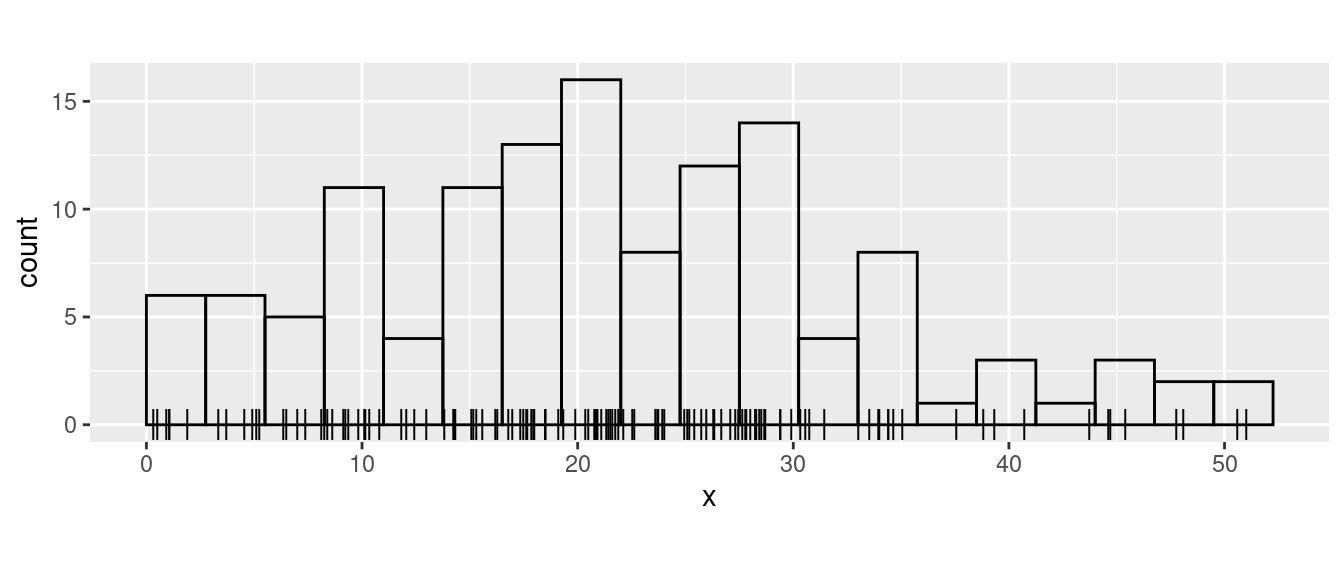

Fiting the model

Build a 1D mesh:

x <- seq(0, 55, length.out = 50)
mesh1D <- fm_mesh_1d(x, boundary = "free")

Make the latent components for a 1D SPDE model, using an integrate-to-zero constraint for better identifiability:

matern <- inla.spde2.pcmatern(mesh1D,
  prior.range = c(150, 0.75),
  prior.sigma = c(0.1, 0.75),
  constr = TRUE
)
comp <- ~ spde1D(x, model = matern) + Intercept(1)

Here we want to fit to the actual points, and the inlabru functions that are used for this are bru() and bru_obs(..., family = "cp"). For this special case there is also a shortcut function lgcp() (for ‘Log Gaussian Cox Process’), but it doesn’t support all features. The standard way of specifying the function space for integration is via the domain argument.

fit.spde <- bru(
  comp,
  bru_obs(x ~ ., family = "cp", data = pts2, domain = list(x = mesh1D))
)
## Equivalent call for this particular example:
# fit.spde <- lgcp(
#   comp,
#   formula = x ~ ., data = pts2, domain = list(x = mesh1D)
# )

Here, formula = x ~ . means that the observed points are in x, and . denotes a linear predictor that is the sum of all the latent components.

SPDE parameters

We can look at the posterior distributions of the parameters of the SPDE using the function spde.posterior. It returns x and y values for a plot of the posterior PDF in a data frame, which can be printed using the plot function. To see the PDF for the range parameter, for example:

post.range <- spde.posterior(fit.spde, name = "spde1D", what = "range")
plot(post.range)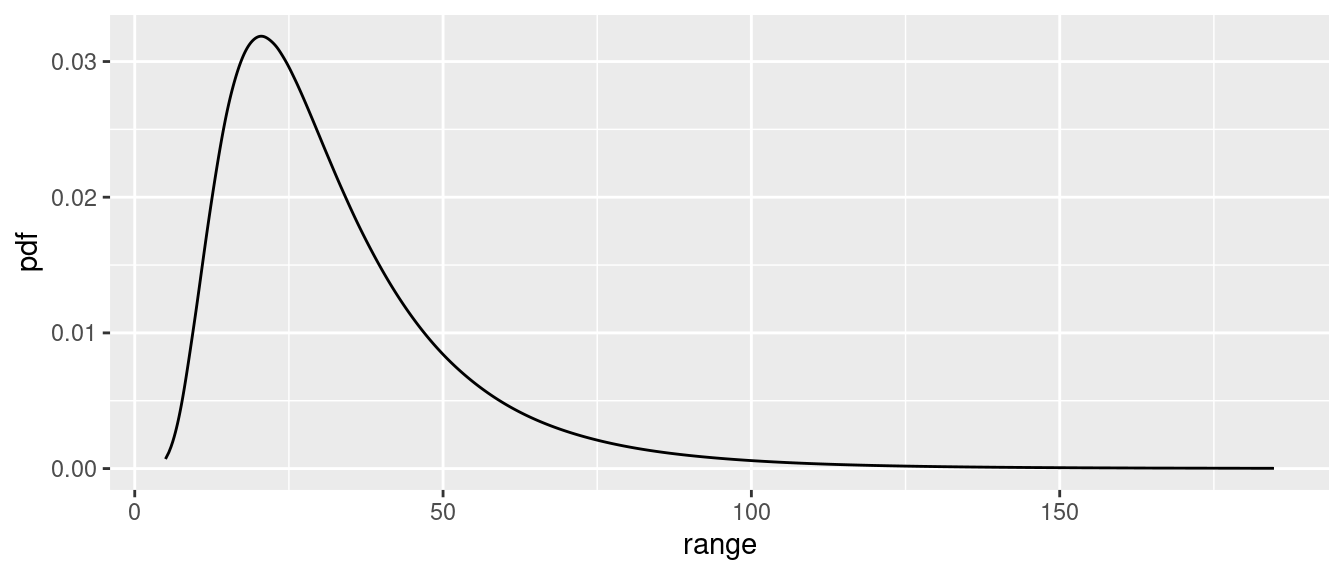

Look at the help file for spde.posterior and then plot the posterior for the log of the SPDE range parameter, the SPDE variance and/or log of the variance, and for the Matern covariance function. Make sure you understand the difference between what is plotted for the range and variance parameters, and for the covariance function (which involves both these parameters).

post.log.range <- spde.posterior(fit.spde,
  name = "spde1D",
  what = "log.range"
)
plot(post.log.range)
post.variance <- spde.posterior(fit.spde,
  name = "spde1D",
  what = "variance"
)
plot(post.variance)
post.log.variance <- spde.posterior(fit.spde,
  name = "spde1D",
  what = "log.variance"
)
plot(post.log.variance)
post.matcorr <- spde.posterior(fit.spde,
  name = "spde1D",
  what = "matern.correlation"
)
plot(post.matcorr)

You can get a feel for sensitivity to priors by specifying different priors and looking at the posterior plots.

Predicting intensity

We can also now predict on any scale we want. For example, to predict on the ‘response’ scale (i.e. the intensity function $\lambda(s)$ ), we call predict thus:

# Set up a data frame of explanatory values at which to predict
predf <- data.frame(x = seq(0, 55, by = 1))
pred_spde <- predict(fit.spde,
  predf,
  ~ exp(spde1D + Intercept),
  n.samples = 1000
)

while to predict on the linear predictor scale (i.e. that of the log intensity, $\log(\lambda(s))$ ), we call predict thus:

pred_spde_lp <- predict(fit.spde, predf, ~ spde1D + Intercept, n.samples = 1000)

here’s how to plot the prediction and 95% credible interval:

plot(pred_spde, color = "red") +
  geom_point(data = pts2, aes(x = x), y = 0, pch = "|", cex = 2) +
  xlab("x") + ylab("Intensity")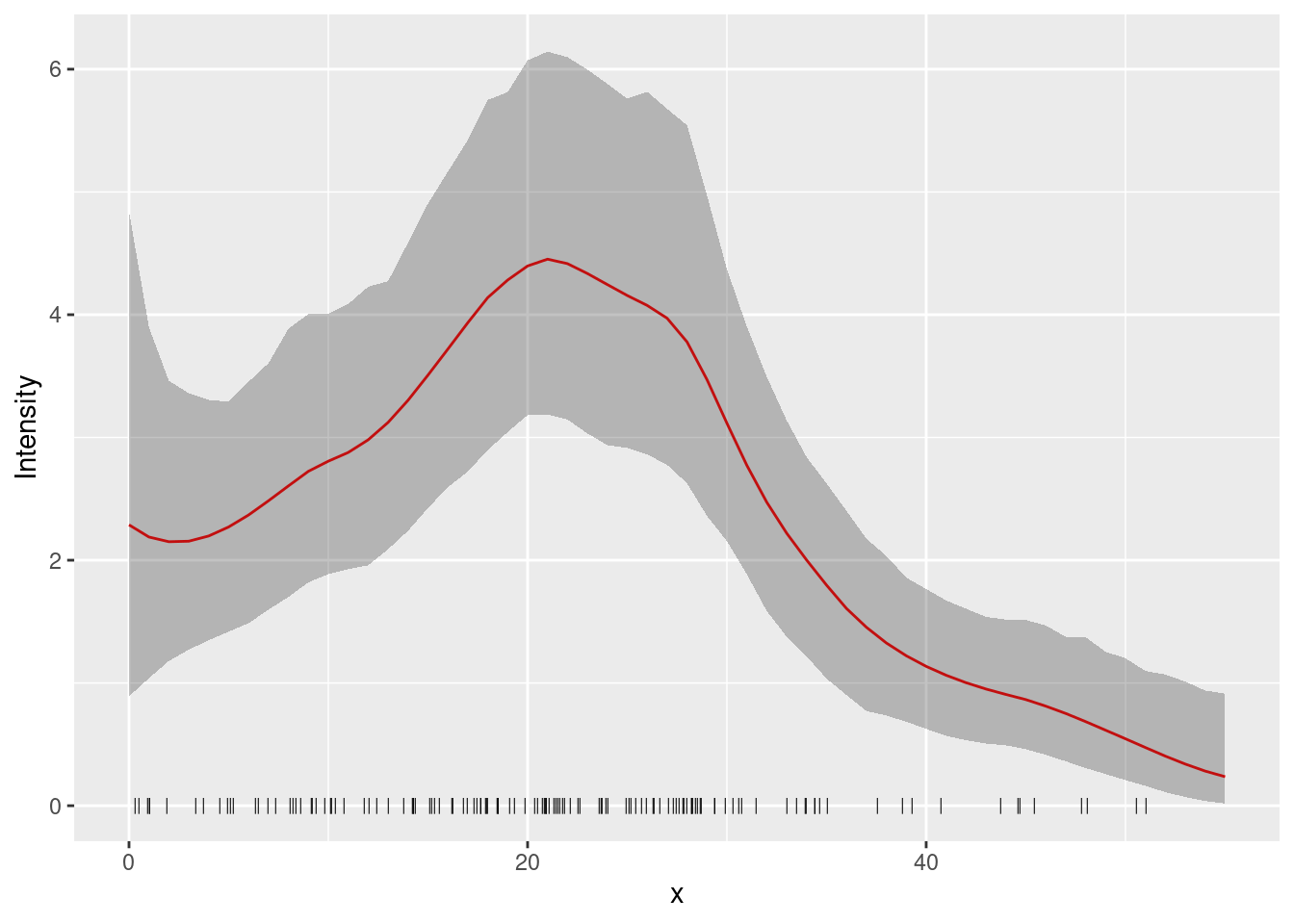

How does this compare with the underlying intensity function that generated the data? The function lambda2_1D( ) in the dataset Poission2_1D calculates the true intensity that was used in simulating these data. In order to plot this, we make a data frame with x- and y-coordinates giving the true intensity function, $\lambda(s)$ . We use lots of x-values to get a nice smooth plot (150 values).

xs <- seq(0, 55, length = 150)
true.lambda <- data.frame(x = xs, y = lambda2_1D(xs))

Plot the fitted and true intensity functions:

plot(pred_spde, color = "red") +
  geom_point(data = pts2, aes(x = x), y = 0, pch = "|", cex = 2) +
  geom_line(data = true.lambda, aes(x, y)) +
  xlab("x") + ylab("Intensity")

Goodness-of-Fit

We can look at the goodness-of-fit of the mode using the inlabru function bincount( ), which plots the 95% credible intervals in a specified set of bins along the x-axis together with the observed count in each bin: The credible intervals are shown as red rectangles, the mean fitted value as a short horizontal blue line, and the observed data as black points:

bc <- bincount(
  result = fit.spde,
  observations = pts2,
  breaks = seq(0, max(pts2), length = 12),
  predictor = x ~ exp(spde1D + Intercept)
)

attributes(bc)$ggp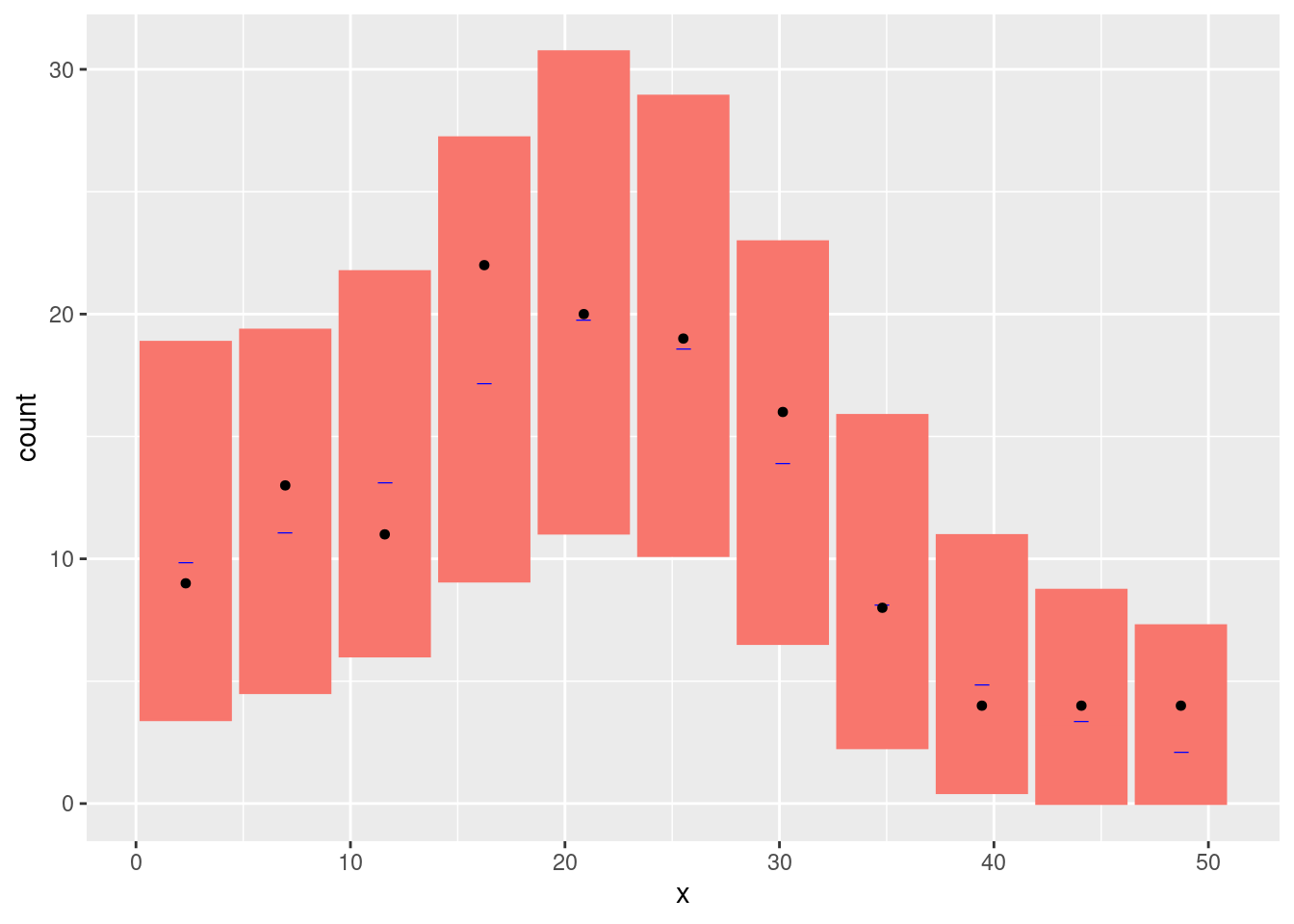

Estimating Abundance

Abundance is the integral of the intensity over space. We estimate it by integrating the predicted intensity over x. Integration is done by adding up the intensity at locations x weighted by a particular weight. The locations x and their weights are constructed using the fm_int function

ips <- fm_int(mesh1D, name = "x")
head(ips)
#>          x    weight .block
#> 1 0.000000 0.1870748      1
#> 2 1.122449 0.3741497      1
#> 3 2.244898 0.3741497      1
#> 4 3.367347 0.3741497      1
#> 5 4.489796 0.3741497      1
#> 6 5.612245 0.3741497      1
Lambda <- predict(fit.spde, ips, ~ sum(weight * exp(spde1D + Intercept)))

You can look at the abundance estimate by typing

Lambda
#>       mean       sd   q0.025     q0.5   q0.975   median sd.mc_std_err mean.mc_std_err
#> 1 129.6223 12.68905 107.4606 127.8858 158.2021 127.8858     0.9380062        1.456506

mean is the posterior mean abundance.
sd is the estimated standard error of the posterior of the abundance.
cv is its estimated coefficient of variation (stander error divided by mean).
q0.025 and q0.975 are the 95% credible interval bounds.
q0.5 is the posterior median abundance

But it is not quite that simple! The above posterior for abundance takes account only of the variance due to us not knowing the parameters of the intensity function. It neglects the variance in the number of point locations, given the intensity function. To include this we need to modify predict( ) as follows:

Nest <- predict(
  fit.spde, ips,
  ~ data.frame(
    N = 50:250,
    dpois = dpois(50:250,
      lambda = sum(weight * exp(spde1D + Intercept))
    )
  )
)

This calculates the same statistics as were calculated for Lambda, but for evey value of N from 50 to 250, rather than for the posterior mean N alone:

Nest[Nest$N %in% 100:105, ]
#>      N        mean          sd       q0.025         q0.5     q0.975       median sd.mc_std_err
#> 51 100 0.003863508 0.006907792 2.039623e-06 0.0009054726 0.02882198 0.0009054726   0.001137718
#> 52 101 0.004424321 0.007441492 3.054114e-06 0.0011661563 0.03089679 0.0011661563   0.001148312
#> 53 102 0.005038000 0.007964208 4.528407e-06 0.0014871753 0.03279623 0.0014871753   0.001143138
#> 54 103 0.005705186 0.008471503 6.649244e-06 0.0018781629 0.03447447 0.0018781629   0.001122253
#> 55 104 0.006425817 0.008959468 9.669555e-06 0.0023491512 0.03589014 0.0023491512   0.001086541
#> 56 105 0.007199044 0.009424691 1.392799e-05 0.0029102846 0.03700809 0.0029102846   0.001037734
#>    mean.mc_std_err
#> 51    0.0009183228
#> 52    0.0009738116
#> 53    0.0010250484
#> 54    0.0010716009
#> 55    0.0011132549
#> 56    0.0011500159

We compute the 95% prediction interval and the median as follows

inla.qmarginal(c(0.025, 0.5, 0.975), marginal = list(x = Nest$N, y = Nest$mean))
#> [1] 100.5689 129.6071 163.6454

Compare Lambda to Nest by plotting: First calculate the posterior conditional on the mean of Lambda

Nest$plugin_estimate <- dpois(Nest$N, lambda = Lambda$mean)

Then plot it and the unconditional posterior

ggplot(data = Nest) +
  geom_point(aes(x = N, y = mean, colour = "Posterior")) +
  geom_line(aes(x = N, y = mean, colour = "Posterior")) +
  geom_ribbon(
    aes(
      x = N,
      ymin = mean - 2 * mean.mc_std_err,
      ymax = mean + 2 * mean.mc_std_err
    ),
    fill = "grey",
    alpha = 0.5
  ) +
  geom_point(aes(x = N, y = plugin_estimate, colour = "Plugin")) +
  geom_line(aes(x = N, y = plugin_estimate, colour = "Plugin")) +
  ylab("pmf")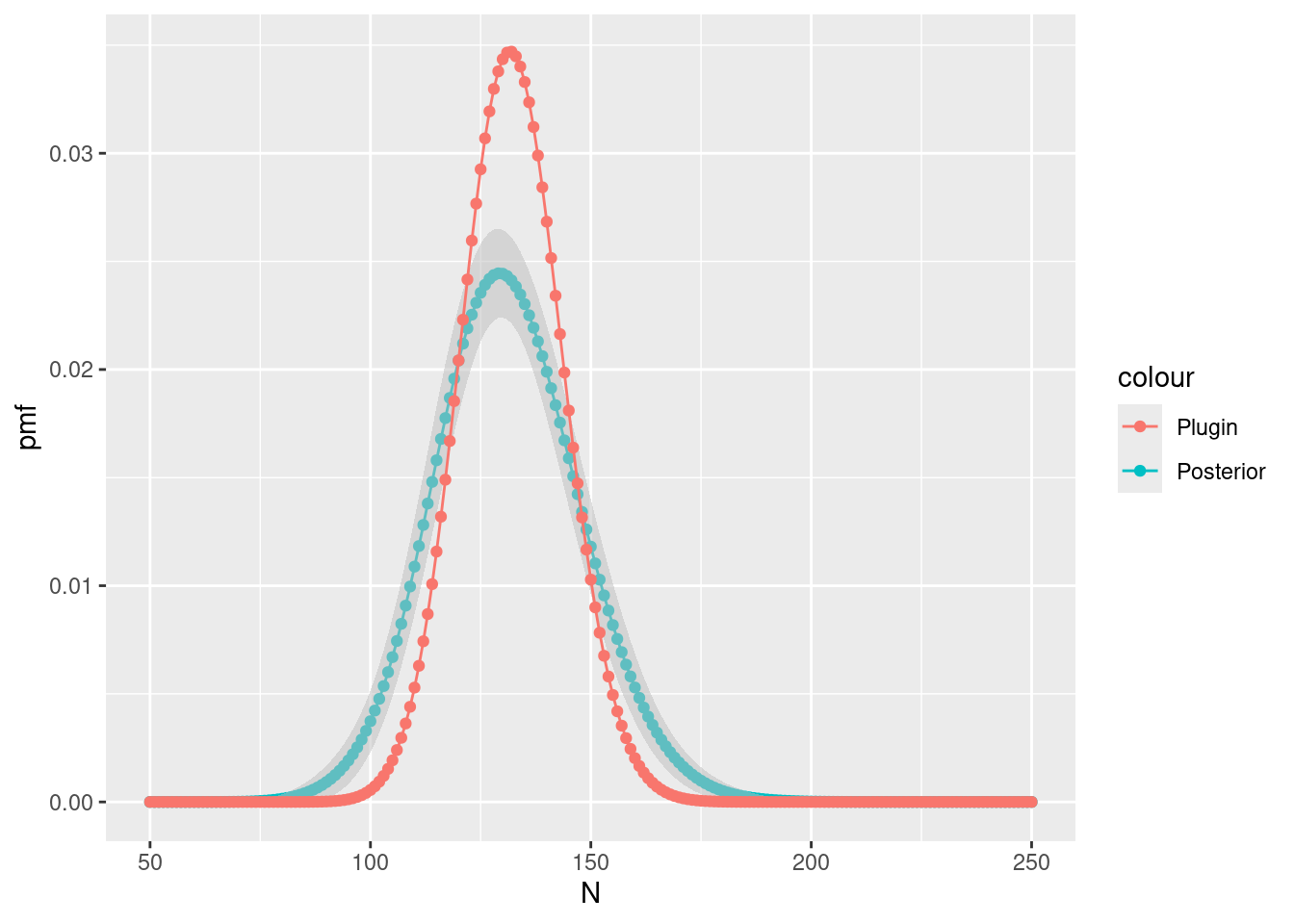

Do the differences make sense to you?

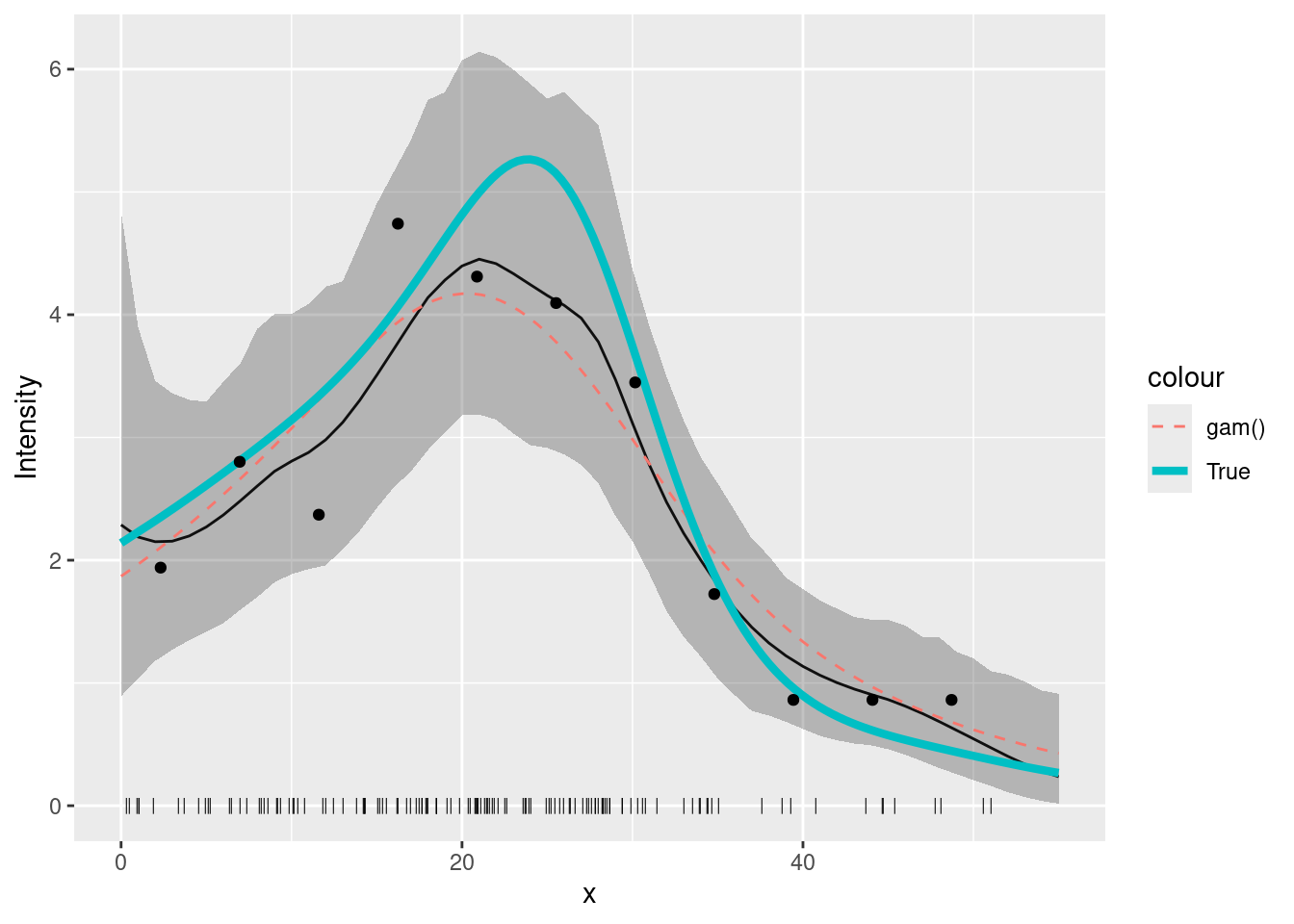
Comparison to GAM fit

Now refit a GAM for the count data of Poisson2_1D and plot the estimated intensity function from this GAM fit, together with the LGCP fitted above and the true intensity.

cd2 <- countdata2
fit2.gam <- gam(count ~ s(x, k = 10) + offset(log(exposure)),
  family = poisson(),
  data = cd2
)
dat4pred <- data.frame(
  x = seq(0, 55, length = 100),
  exposure = rep(cd2$exposure[1], 100)
)
pred2.gam <- predict(fit2.gam, newdata = dat4pred, type = "response")
dat4pred2 <- cbind(dat4pred, gam = pred2.gam)

You should get a plot like this (thick line is the true intensity, the thin solid line the inlabru fit, the dashed line the GAM fit:

plot(pred_spde) +
  geom_point(data = pts2, aes(x = x), y = 0, pch = "|", cex = 2) +
  geom_line(
    data = dat4pred2,
    aes(x, gam / exposure, colour = "gam()"),
    lty = 2
  ) +
  geom_line(data = true.lambda, aes(x, y, colour = "True"), lwd = 1.5) +
  geom_point(data = cd2, aes(x, y = count / exposure)) +
  ylab("Intensity") + xlab("x")

LGCPs - An example in one dimension

David Borchers and Finn Lindgren

Generated on 2024-12-18