Nonlinear model approximation

See the method vignette for details of the general inlabru method. Here, we’ll take a look at a small toy example to see the difference between a few posterior approximation methods.

Note: This vignette is not completed yet.

A small toy problem

Hierarchical model: $$\begin{aligned} \lambda &\sim \mathsf{Exp}(\gamma) \\ (y_i|\lambda) &\sim \mathsf{Po}(\lambda), \text{ independent across $i=1,\dots,n$} \end{aligned}$$ With $\overline{y}=\frac{1}{n}\sum_{i=1}^n y_i$, the posterior density is $$\begin{aligned} p(\lambda | \{y_i\}) &\propto p(\lambda, y_1,\dots,y_n) \\ &\propto \exp(-\gamma\lambda) \exp(-n\lambda) \lambda^{n\overline{y}} \\ &= \exp\{-(\gamma+n)\lambda\} \lambda^{n\overline{y}}, \end{aligned}$$ which is the density of a $\mathsf{Ga}(\alpha = 1+n\overline{y}, \beta = \gamma+n)$ distribution.

Latent Gaussian predictor version

Introducing a latent Gaussian variable $u\sim\mathsf{N}(0,1)$, the model can be reformulated as $$\begin{aligned} \lambda(u) &=-\ln\{1-\Phi(u)\}/\gamma \\ (y_i|u) &\sim \mathsf{Po}(\lambda(u)) \end{aligned}$$ We will need some derivatives of $\lambda$ with respect to $u$: $$\begin{aligned} \frac{\partial\lambda(u)}{\partial u} &= \frac{1}{\gamma}\frac{\phi(u)}{1-\Phi(u)} = \lambda'(u) \\ \frac{\partial^2\lambda(u)}{\partial u^2} &= - \frac{1}{\gamma}\frac{\phi(u)}{1-\Phi(u)} \left( u + \frac{\phi(u)}{1-\Phi(u)} \right) = -\lambda'(u)\left\{u-\gamma\lambda'(u)\right\} \\ \frac{\partial\ln\lambda(u)}{\partial u} &= \frac{1}{\lambda(u)} \frac{\partial\lambda(u)}{\partial u} =\frac{1}{-\ln\{1-\Phi(u)\}} \frac{\phi(u)}{1-\Phi(u)} = \frac{\lambda'(u)}{\lambda(u)} \\ \frac{\partial^2\ln\lambda(u)}{\partial u^2} &= \frac{1}{\lambda(u)} \frac{\partial^2\lambda(u)}{\partial u^2} -\frac{1}{\lambda(u)^2} \left(\frac{\partial\lambda(u)}{\partial u}\right)^2 = \frac{-\lambda'(u)\{u - \gamma\lambda'(u)\}}{\lambda(u)} - \frac{\lambda'(u)^2}{\lambda(u)^2}\\ &= -\frac{\lambda'(u)}{\lambda(u)}\left\{ u - \gamma\lambda'(u) +\frac{\lambda'(u)}{\lambda(u)} \right\} \end{aligned}$$

lambda <- function(u, gamma) {
  -pnorm(u, lower.tail = FALSE, log.p = TRUE) / gamma
}
lambda_inv <- function(lambda, gamma) {
  qnorm(-lambda * gamma, lower.tail = FALSE, log.p = TRUE)
}
D1lambda <- function(u, gamma) {
  exp(dnorm(u, log = TRUE) - pnorm(u, lower.tail = FALSE, log.p = TRUE)) / gamma
}
D2lambda <- function(u, gamma) {
  D1L <- D1lambda(u, gamma)
  -D1L * (u - gamma * D1L)
}
D1log_lambda <- function(u, gamma) {
  D1lambda(u, gamma) / lambda(u, gamma)
}
D2log_lambda <- function(u, gamma) {
  D1logL <- D1log_lambda(u, gamma)
  -D1logL * (u - gamma * D1lambda(u, gamma = gamma) + D1logL)
}

Latent Gaussian posterior approximations

A basic approximation of the posterior distribution for $\lambda$ given $y$ can be defined as a deterministic transformation of a Gaussian distribution obtained from a 2nd order Taylor approximation of $\ln p(u|\{y_i\})$ at the posterior mode $u_0$ of $p(u|\{y_i\})$. The needed derivatives are $$\begin{aligned} \frac{\partial\ln p(u|\{y_i\})}{\partial u} &= \frac{\partial\ln\phi(u)}{\partial u} - n\lambda'(u) + n\overline{y}\frac{\lambda'(u)}{\lambda(u)} = -u + n\frac{\lambda'(u)}{\lambda(u)}\left\{ \overline{y} - \lambda(u) \right\} \\ \frac{\partial^2\ln p(u|\{y_i\})}{\partial u^2} &= -1 - n \frac{\lambda'(u)}{\lambda(u)}\left\{ u - \gamma\lambda'(u) + \frac{\lambda'(u)}{\lambda(u)} \right\} \left\{ \overline{y} - \lambda(u) \right\} - n \frac{\lambda'(u)^2}{\lambda(u)} \end{aligned}$$ At the mode $u_0$, the first order derivative is zero, and $$\begin{aligned} \left.\frac{\partial^2\ln p(u|\{y_i\})}{\partial u^2}\right|_{u=u_0} &= -1 - \left\{ u_0 - \gamma\lambda'(u_0) + \frac{\lambda'(u_0)}{\lambda(u_0)} \right\} u_0 - n \frac{\lambda'(u_0)^2}{\lambda(u_0)} . \end{aligned}$$ The quadratic approximation of the log-posterior density at the mode $u_0$ is then $$\ln \breve{p}(u|\{y_i\}) = \text{const} - \frac{(u-u_0)^2}{2} \left[ - \left.\frac{\partial^2\ln p(u|\{y_i\})}{\partial u^2}\right|_{u=u_0} \right]$$ In inlabru, the approximation first linearises $\ln \lambda(u)$ at $u_0$ before applying the Taylor approximation of $\ln p(u|\{y_i\})$. The linearised log-predictor is $$\ln \overline{\lambda}(u) = \ln \lambda(u_0) + \frac{\lambda'(u_0)}{\lambda(u_0)}(u - u_0)$$ so that $$\overline{\lambda}'(u) = \frac{\lambda'(u_0)}{\lambda(u_0)} \overline{\lambda}(u)$$ and the second order derivative of the linearised log-posterior density is $$\begin{aligned} \left.\frac{\partial^2\ln \overline{p}(u|\{y_i\})}{\partial u^2}\right|_{u=u_0} &= -1 - n \frac{\lambda'(u_0)^2}{\lambda(u_0)} . \end{aligned}$$

log_p <- function(u, y, gamma) {
  L <- lambda(u, gamma)
  n <- length(y)
  dnorm(u, log = TRUE) - n * L + n * mean(y) * log(L) - sum(lgamma(y + 1))
}
D1log_p <- function(u, y, gamma) {
  n <- length(y)
  -u + n * D1log_lambda(u, gamma) * (mean(y) - lambda(u, gamma))
}
D2log_p <- function(u, y, gamma) {
  n <- length(y)
  -1 +
    n * D2log_lambda(u, gamma) * (mean(y) - lambda(u, gamma)) -
    n * D1log_lambda(u, gamma) * D1lambda(u, gamma)
}

g <- 1
y <- c(0, 1, 2)
y <- c(0, 0, 0, 0, 0)
y <- rpois(5, 5)
mu_quad <- uniroot(
  D1log_p,
  lambda_inv((1 + sum(y)) / (g + length(y)) * c(1 / 10, 10), gamma = g),
  y = y, gamma = g
)$root
sd_quad <- (-D2log_p(mu_quad, y = y, gamma = g))^-0.5
sd_lin <- (1 + length(y) * D1log_lambda(mu_quad, gamma = g)^2 *
  lambda(mu_quad, gamma = g))^-0.5
lambda0 <- lambda(mu_quad, gamma = g)

Posterior densities

ggplot() +
  xlim(
    lambda(mu_quad - 4 * sd_quad, gamma = g),
    lambda(mu_quad + 4 * sd_quad, gamma = g)
  ) +
  xlab("lambda") +
  ylab("Density") +
  geom_function(
    fun = function(x) {
      exp(log_p(lambda_inv(x, gamma = g), y = y, gamma = g)) /
        D1lambda(lambda_inv(x, gamma = g), gamma = g) / (
          exp(log_p(lambda_inv(lambda0, gamma = g), y = y, gamma = g)) /
            D1lambda(lambda_inv(lambda0, gamma = g), gamma = g)
        ) *
        dgamma(lambda0, shape = 1 + sum(y), rate = g + length(y))
    },
    mapping = aes(col = "Theory"),
    n = 1000
  ) +
  geom_function(
    fun = dgamma,
    args = list(shape = 1 + sum(y), rate = g + length(y)),
    mapping = aes(col = "Theory"),
    n = 1000
  ) +
  geom_function(
    fun = function(x) {
      dnorm(lambda_inv(x, gamma = g), mean = mu_quad, sd = sd_quad) /
        D1lambda(lambda_inv(x, gamma = g), gamma = g)
    },
    mapping = aes(col = "Quadratic"),
    n = 1000
  ) +
  geom_function(
    fun = function(x) {
      dnorm(lambda_inv(x, gamma = g), mean = mu_quad, sd = sd_lin) /
        D1lambda(lambda_inv(x, gamma = g), gamma = g)
    },
    mapping = aes(col = "Linearised"),
    n = 1000
  ) +
  geom_vline(mapping = aes(
    xintercept = (1 + sum(y)) / (g + length(y)),
    lty = "Bayes mean"
  )) +
  geom_vline(mapping = aes(xintercept = lambda0, lty = "Bayes mode")) +
  geom_vline(mapping = aes(xintercept = mean(y), lty = "Plain mean"))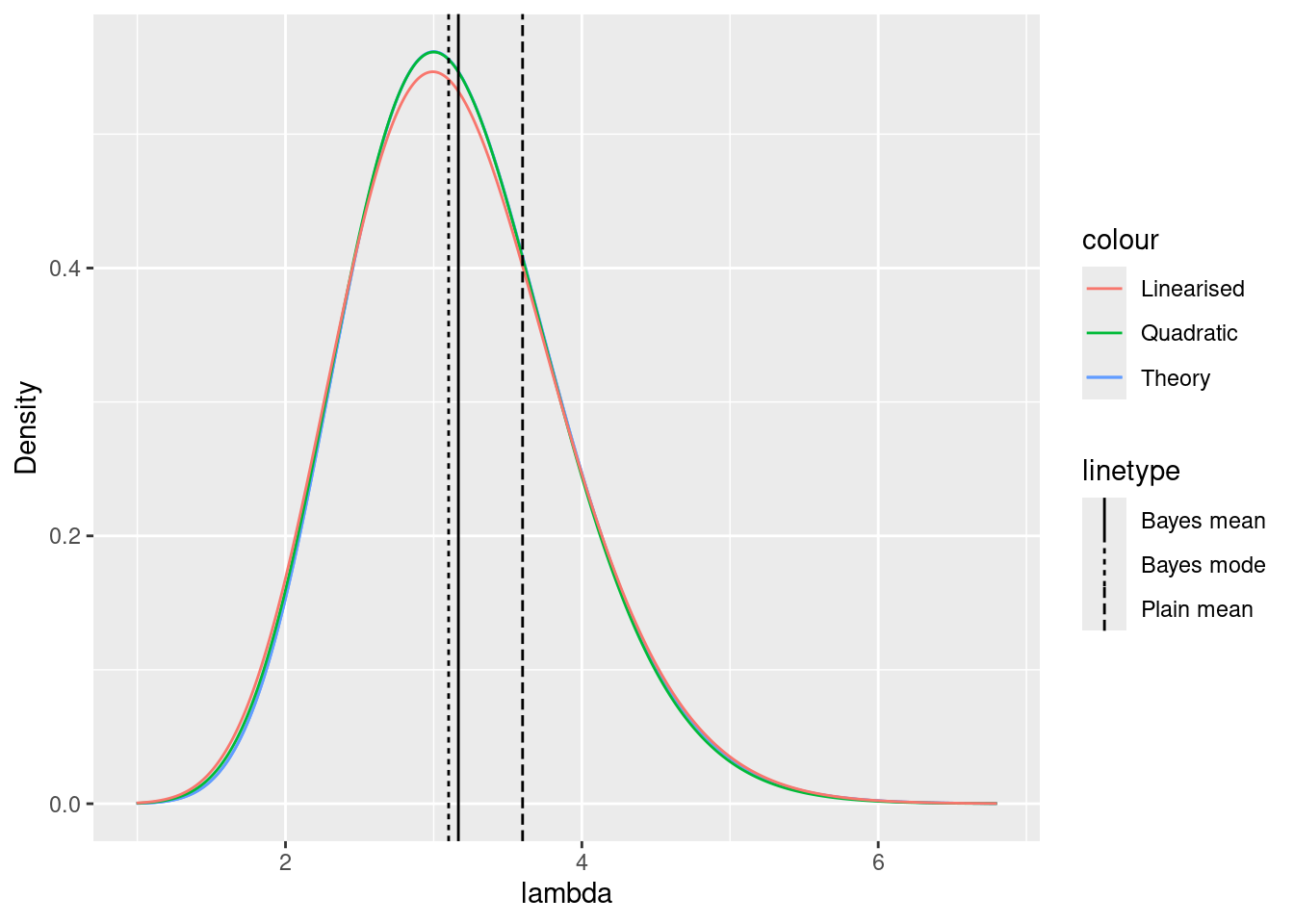

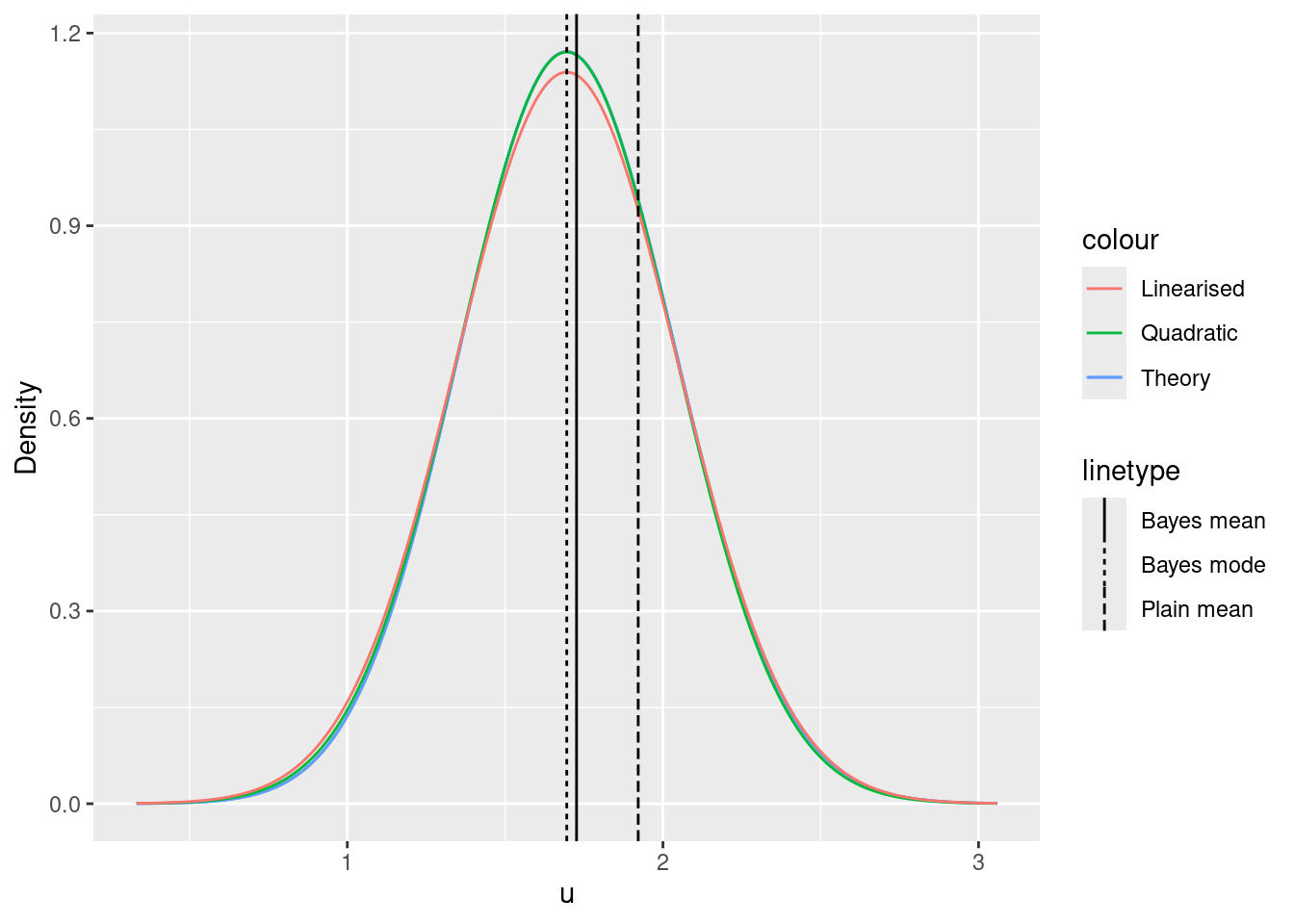
ggplot() +
  xlim(
    lambda_inv(lambda0, gamma = g) - 4 * sd_quad,
    lambda_inv(lambda0, gamma = g) + 4 * sd_quad
  ) +
  xlab("u") +
  ylab("Density") +
  geom_function(
    fun = function(x) {
      exp(log_p(x, y = y, gamma = g) -
        log_p(lambda_inv(lambda0, gamma = g), y = y, gamma = g)) *
        (dgamma(lambda0, shape = 1 + sum(y), rate = g + length(y)) *
          D1lambda(lambda_inv(lambda0, gamma = g), gamma = g))
    },
    mapping = aes(col = "Theory"),
    n = 1000
  ) +
  geom_function(
    fun = function(x) {
      dgamma(lambda(x, gamma = g), shape = 1 + sum(y), rate = g + length(y)) *
        D1lambda(x, gamma = g)
    },
    mapping = aes(col = "Theory"),
    n = 1000
  ) +
  geom_function(
    fun = dnorm,
    args = list(mean = mu_quad, sd = sd_quad),
    mapping = aes(col = "Quadratic"),
    n = 1000
  ) +
  geom_function(
    fun = dnorm,
    args = list(mean = mu_quad, sd = sd_lin),
    mapping = aes(col = "Linearised"),
    n = 1000
  ) +
  geom_vline(
    mapping = aes(
      xintercept = lambda_inv((1 + sum(y)) / (g + length(y)),
        gamma = g
      ),
      lty = "Bayes mean"
    )
  ) +
  geom_vline(
    mapping = aes(
      xintercept = lambda_inv(lambda0, gamma = g),
      lty = "Bayes mode"
    )
  ) +
  geom_vline(
    mapping = aes(
      xintercept = lambda_inv(mean(y), gamma = g),
      lty = "Plain mean"
    )
  )

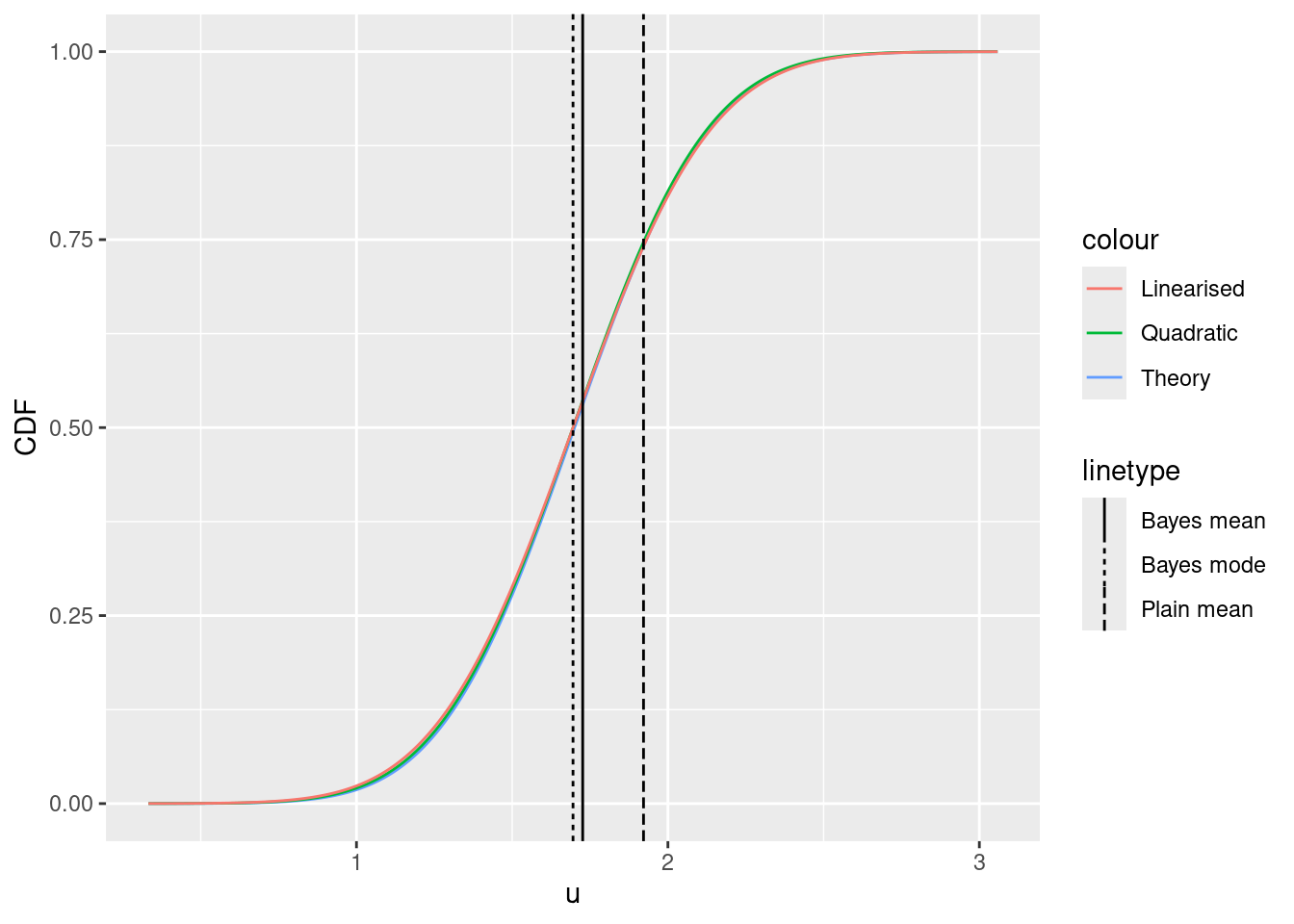
Posterior CDFs

ggplot() +
  xlim(
    lambda(mu_quad - 4 * sd_quad, gamma = g),
    lambda(mu_quad + 4 * sd_quad, gamma = g)
  ) +
  xlab("lambda") +
  ylab("CDF") +
  geom_function(
    fun = pgamma,
    args = list(shape = 1 + sum(y), rate = g + length(y)),
    mapping = aes(col = "Theory"),
    n = 1000
  ) +
  geom_function(
    fun = function(x) {
      pnorm(lambda_inv(x, gamma = g), mean = mu_quad, sd = sd_quad)
    },
    mapping = aes(col = "Quadratic"),
    n = 1000
  ) +
  geom_function(
    fun = function(x) {
      pnorm(lambda_inv(x, gamma = g), mean = mu_quad, sd = sd_lin)
    },
    mapping = aes(col = "Linearised"),
    n = 1000
  ) +
  geom_vline(mapping = aes(
    xintercept = (1 + sum(y)) / (g + length(y)),
    lty = "Bayes mean"
  )) +
  geom_vline(mapping = aes(xintercept = lambda0, lty = "Bayes mode")) +
  geom_vline(mapping = aes(xintercept = mean(y), lty = "Plain mean"))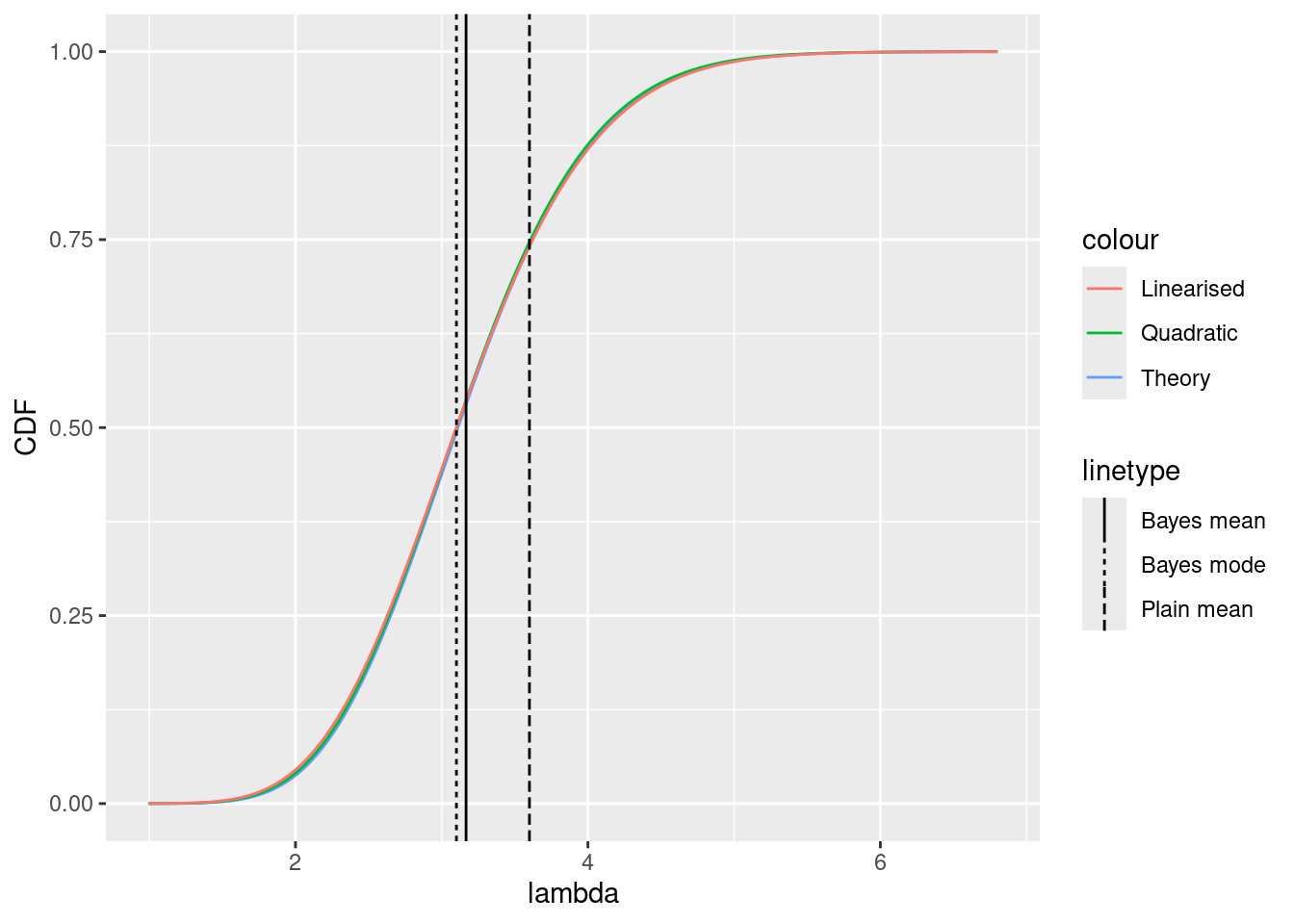

ggplot() +
  xlim(
    lambda_inv(lambda0, gamma = g) - 4 * sd_quad,
    lambda_inv(lambda0, gamma = g) + 4 * sd_quad
  ) +
  xlab("u") +
  ylab("CDF") +
  geom_function(
    fun = function(x) {
      pgamma(lambda(x, gamma = g), shape = 1 + sum(y), rate = g + length(y))
    },
    mapping = aes(col = "Theory"),
    n = 1000
  ) +
  geom_function(
    fun = pnorm,
    args = list(mean = mu_quad, sd = sd_quad),
    mapping = aes(col = "Quadratic"),
    n = 1000
  ) +
  geom_function(
    fun = pnorm,
    args = list(mean = mu_quad, sd = sd_lin),
    mapping = aes(col = "Linearised"),
    n = 1000
  ) +
  geom_vline(mapping = aes(
    xintercept = lambda_inv((1 + sum(y)) / (g + length(y)),
      gamma = g
    ),
    lty = "Bayes mean"
  )) +
  geom_vline(mapping = aes(
    xintercept = lambda_inv(lambda0, gamma = g),
    lty = "Bayes mode"
  )) +
  geom_vline(mapping = aes(
    xintercept = lambda_inv(mean(y), gamma = g),
    lty = "Plain mean"
  ))