LGCPs - Multiple Likelihoods • inlabru

Introduction

For this vignette we are going to be working with the inlabru’s ´gorillas_sf´ dataset which was originally obtained from the R package spatstat. The data set contains two types of gorillas nests which are marked as either major or minor. We will set up a multi-likelihood model for these nests which creates two spatial LGCPs that share a common intercept but have employ different spatial smoothers.

Setting things up

Load libraries

library(inlabru)
library(INLA)
library(ggplot2)
bru_safe_sp(force = TRUE)

Get the data

For the next few practicals we are going to be working with a dataset obtained from the R package spatstat, which contains the locations of 647 gorilla nests. We load the dataset like this:

data(gorillas_sf, package = "inlabru")

Plot the nests and visualize the group membership (major/minor) by color:

ggplot() +
  gg(gorillas_sf$mesh) +
  gg(gorillas_sf$nests, aes(color = group)) +
  gg(gorillas_sf$boundary, alpha = 0) +
  ggtitle("Gorillas nests and group membership")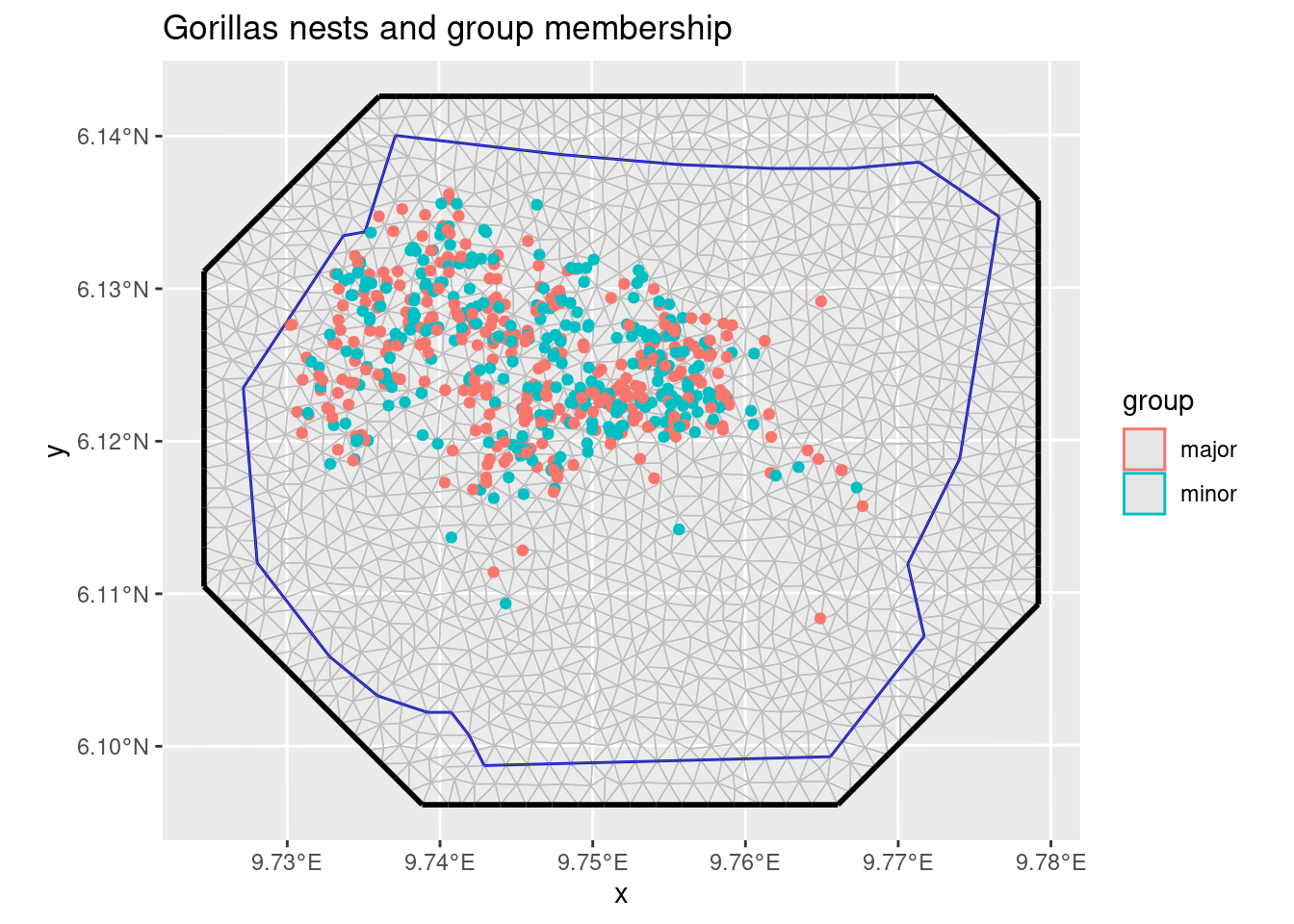

Fiting the model

First, we define all components that enter the joint model. That is, the intercept that is common to both LGCPs and the two different spatial smoothers, one for each nest group.

matern <- inla.spde2.pcmatern(gorillas_sf$mesh,
  prior.range = c(0.1, 0.01),
  prior.sigma = c(1, 0.01)
)

cmp <- ~
  Common(geometry, model = matern) +
    Difference(geometry, model = matern) +
    Intercept(1)

Given these components we define the linear predictor for each of the likelihoods. (Using “.” indicates a pure additive model, and one can use include/exclude options for bru_obs() to indicate which components are actively involved in each model.)

fml.major <- geometry ~ Intercept + Common + Difference / 2
fml.minor <- geometry ~ Intercept + Common - Difference / 2

Setting up the Cox process likelihoods is easy in this example. Both nest types were observed within the same window:

lik_minor <- bru_obs("cp",
  formula = fml.major,
  data = gorillas_sf$nests[gorillas_sf$nests$group == "major", ],
  samplers = gorillas_sf$boundary,
  domain = list(geometry = gorillas_sf$mesh)
)
lik_major <- bru_obs("cp",
  formula = fml.minor,
  data = gorillas_sf$nests[gorillas_sf$nests$group == "minor", ],
  samplers = gorillas_sf$boundary,
  domain = list(geometry = gorillas_sf$mesh)
)

… which we provide to the ´bru´ function.

jfit <- bru(cmp, lik_major, lik_minor,
  options = list(
    control.inla = list(
      int.strategy = "eb"
    ),
    bru_max_iter = 1
  )
)

library(patchwork)
pl.major <- ggplot() +
  gg(gorillas_sf$mesh,
    mask = gorillas_sf$boundary,
    col = exp(jfit$summary.random$Common$mean)
  )
pl.minor <- ggplot() +
  gg(gorillas_sf$mesh,
    mask = gorillas_sf$boundary,
    col = exp(jfit$summary.random$Difference$mean)
  )
(pl.major + scale_fill_continuous(trans = "log")) +
  (pl.minor + scale_fill_continuous(trans = "log")) &
  theme(legend.position = "right")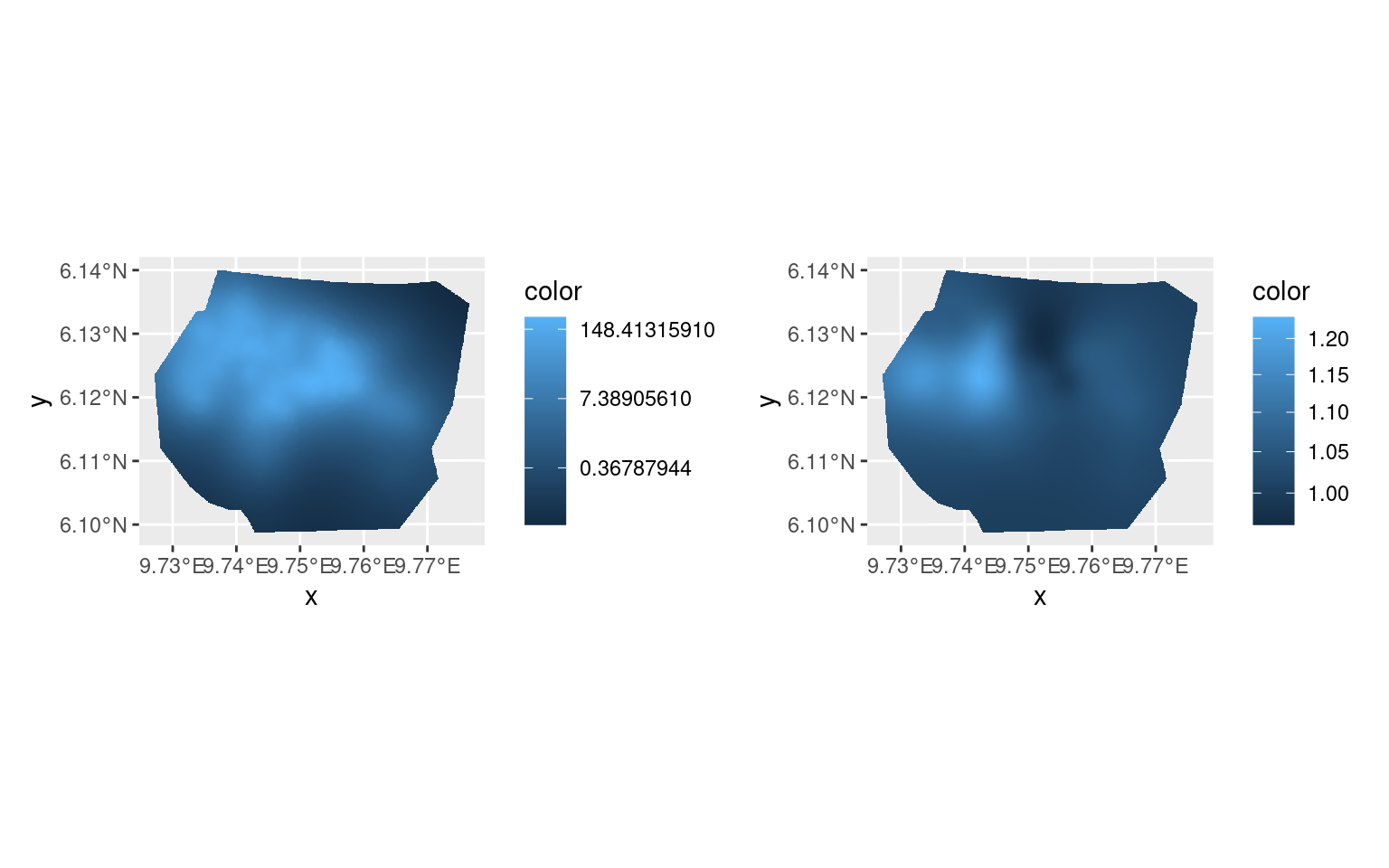

Rerunning

Rerunning with the previous estimate as starting point sometimes improves the accuracy of the posterior distribution estimation.

jfit0 <- jfit
jfit <- bru_rerun(jfit)

pl.major <- ggplot() +
  gg(gorillas_sf$mesh,
    mask = gorillas_sf$boundary,
    col = exp(jfit$summary.random$Common$mean)
  )
pl.minor <- ggplot() +
  gg(gorillas_sf$mesh,
    mask = gorillas_sf$boundary,
    col = exp(jfit$summary.random$Difference$mean)
  )
(pl.major + scale_fill_continuous(trans = "log")) +
  (pl.minor + scale_fill_continuous(trans = "log")) &
  theme(legend.position = "right")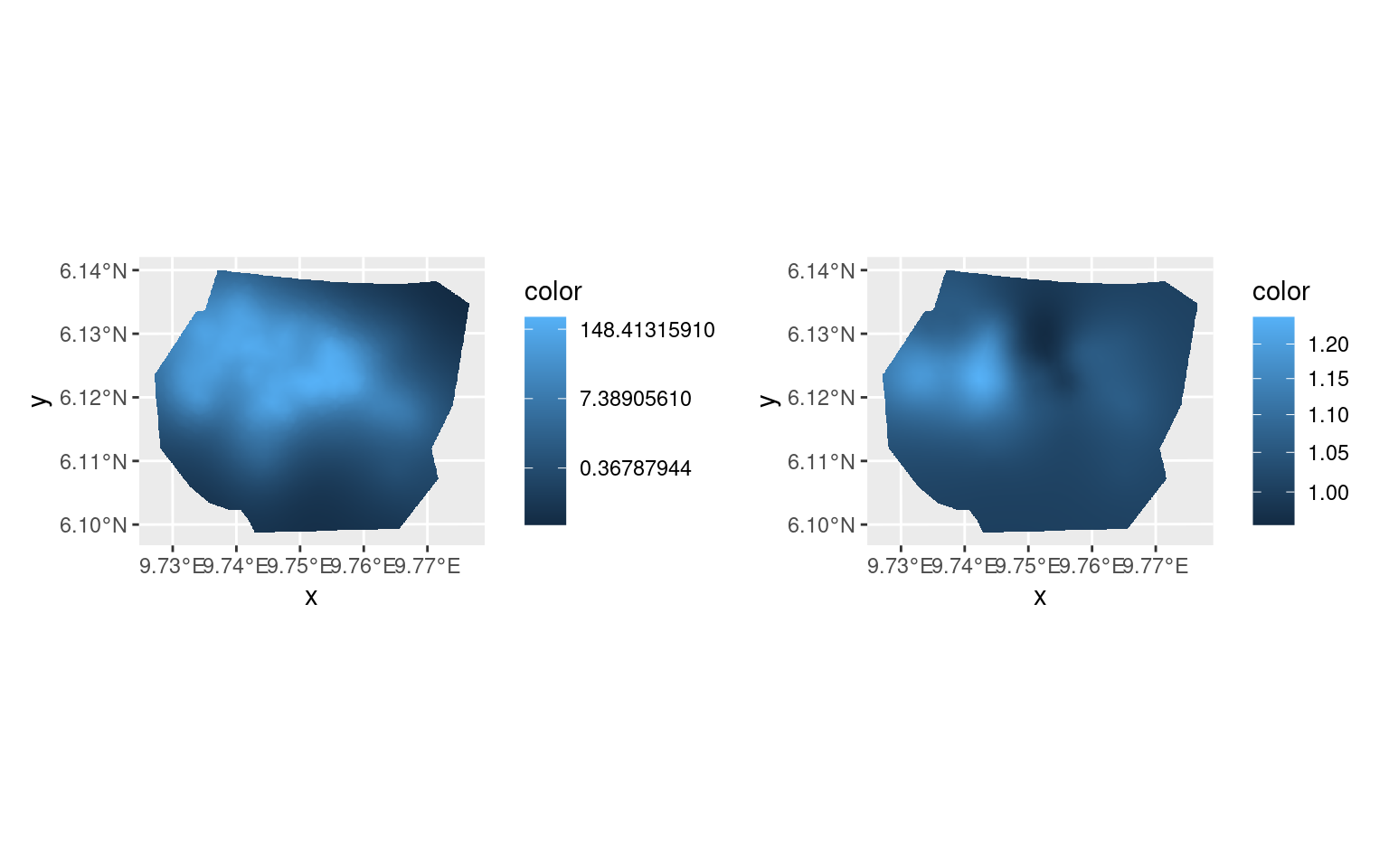

summary(jfit0)
#> inlabru version: 2.12.0.9001
#> INLA version: 24.12.11
#> Components:
#> Common: main = spde(geometry), group = exchangeable(1L), replicate = iid(1L), NULL
#> Difference: main = spde(geometry), group = exchangeable(1L), replicate = iid(1L), NULL
#> Intercept: main = linear(1), group = exchangeable(1L), replicate = iid(1L), NULL
#> Likelihoods:
#>   Family: 'cp'
#>     Tag: ''
#>     Data class: 'sf', 'data.frame'
#>     Response class: 'numeric'
#>     Predictor: geometry ~ Intercept + Common - Difference/2
#>     Used components: effects[Common, Difference, Intercept], latent[]
#>   Family: 'cp'
#>     Tag: ''
#>     Data class: 'sf', 'data.frame'
#>     Response class: 'numeric'
#>     Predictor: geometry ~ Intercept + Common + Difference/2
#>     Used components: effects[Common, Difference, Intercept], latent[]
#> Time used:
#>     Pre = 0.708, Running = 29.1, Post = 0.178, Total = 29.9 
#> Fixed effects:
#>             mean    sd 0.025quant 0.5quant 0.975quant   mode kld
#> Intercept -0.345 1.371     -3.032   -0.345      2.343 -0.345   0
#> 
#> Random effects:
#>   Name     Model
#>     Common SPDE2 model
#>    Difference SPDE2 model
#> 
#> Model hyperparameters:
#>                       mean    sd 0.025quant 0.5quant 0.975quant  mode
#> Range for Common     2.935 0.572      1.996    2.872      4.241 2.736
#> Stdev for Common     2.047 0.332      1.484    2.016      2.790 1.947
#> Range for Difference 2.017 2.875      0.123    1.146      9.261 0.323
#> Stdev for Difference 0.158 0.097      0.034    0.136      0.399 0.092
#> 
#> Deviance Information Criterion (DIC) ...............: 589.86
#> Deviance Information Criterion (DIC, saturated) ....: 588.21
#> Effective number of parameters .....................: -773.92
#> 
#> Watanabe-Akaike information criterion (WAIC) ...: 1628.75
#> Effective number of parameters .................: 105.01
#> 
#> Marginal log-Likelihood:  -1203.98 
#>  is computed 
#> Posterior summaries for the linear predictor and the fitted values are computed
#> (Posterior marginals needs also 'control.compute=list(return.marginals.predictor=TRUE)')

summary(jfit)
#> inlabru version: 2.12.0.9001
#> INLA version: 24.12.11
#> Components:
#> Common: main = spde(geometry), group = exchangeable(1L), replicate = iid(1L), NULL
#> Difference: main = spde(geometry), group = exchangeable(1L), replicate = iid(1L), NULL
#> Intercept: main = linear(1), group = exchangeable(1L), replicate = iid(1L), NULL
#> Likelihoods:
#>   Family: 'cp'
#>     Tag: ''
#>     Data class: 'sf', 'data.frame'
#>     Response class: 'numeric'
#>     Predictor: geometry ~ Intercept + Common - Difference/2
#>     Used components: effects[Common, Difference, Intercept], latent[]
#>   Family: 'cp'
#>     Tag: ''
#>     Data class: 'sf', 'data.frame'
#>     Response class: 'numeric'
#>     Predictor: geometry ~ Intercept + Common + Difference/2
#>     Used components: effects[Common, Difference, Intercept], latent[]
#> Time used:
#>     Pre = 0.579, Running = 10.4, Post = 0.151, Total = 11.1 
#> Fixed effects:
#>             mean    sd 0.025quant 0.5quant 0.975quant   mode kld
#> Intercept -0.343 1.367     -3.022   -0.343      2.336 -0.343   0
#> 
#> Random effects:
#>   Name     Model
#>     Common SPDE2 model
#>    Difference SPDE2 model
#> 
#> Model hyperparameters:
#>                       mean    sd 0.025quant 0.5quant 0.975quant  mode
#> Range for Common     2.936 0.573      1.999    2.872      4.244 2.733
#> Stdev for Common     2.047 0.332      1.486    2.015      2.791 1.945
#> Range for Difference 2.024 2.779      0.139    1.184      9.073 0.370
#> Stdev for Difference 0.158 0.093      0.035    0.138      0.387 0.096
#> 
#> Deviance Information Criterion (DIC) ...............: 590.38
#> Deviance Information Criterion (DIC, saturated) ....: 588.74
#> Effective number of parameters .....................: -773.52
#> 
#> Watanabe-Akaike information criterion (WAIC) ...: 1629.23
#> Effective number of parameters .................: 105.28
#> 
#> Marginal log-Likelihood:  -1204.05 
#>  is computed 
#> Posterior summaries for the linear predictor and the fitted values are computed
#> (Posterior marginals needs also 'control.compute=list(return.marginals.predictor=TRUE)')

Single-likelihood version

In this particular model, we can also rewrite the problem as a single point process over a product domain over space and group. In versions <= 2.7.0, the integration domain had to be numeric, so we convert the group variable to a 0/1 variable, group_major <- group == "major", which is also useful in the predictor expression:

fml.joint <-
  geometry + group_major ~ Intercept + Common + (group_major - 0.5) * Difference

gorillas_sf$nests$group_major <- gorillas_sf$nests$group == "major"
lik_joint <- bru_obs("cp",
  formula = fml.joint,
  data = gorillas_sf$nests,
  samplers = gorillas_sf$boundary,
  domain = list(
    geometry = gorillas_sf$mesh,
    group_major = c(0, 1)
  )
)

# Approximate with "eb" for faster vignette
jfit_joint <- bru(cmp, lik_joint,
  options = list(
    control.inla = list(
      int.strategy = "eb"
    ),
    bru_max_iter = 1
  )
)

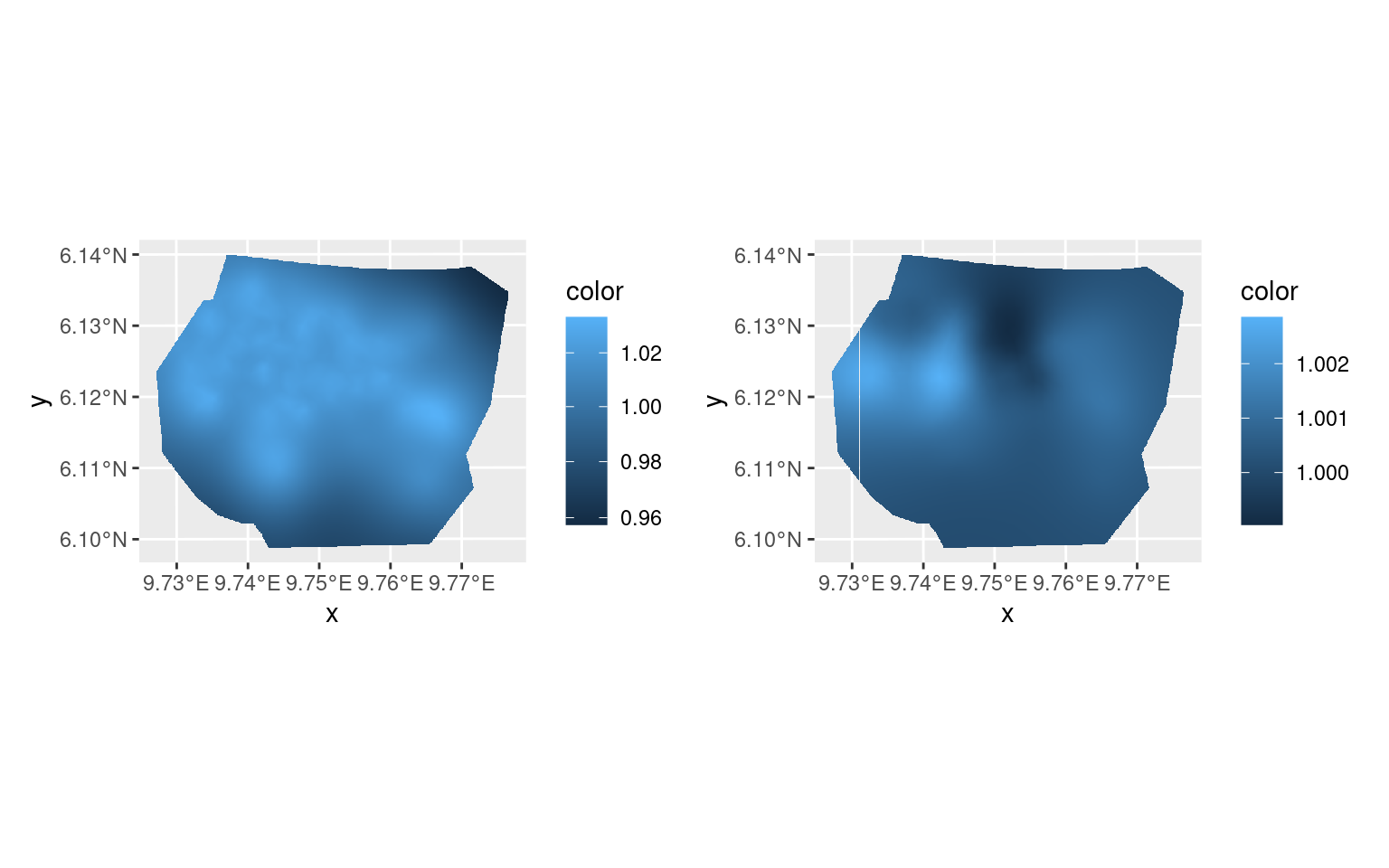
Plotting the ratios of exp(Common) and exp(Difference) between the new fit and the old confirms that the results are the same up to small numerical differences.

library(patchwork)
pl.major <- ggplot() +
  gg(gorillas_sf$mesh,
    mask = gorillas_sf$boundary,
    col = exp(jfit_joint$summary.random$Common$mean -
      jfit$summary.random$Common$mean)
  )
pl.minor <- ggplot() +
  gg(gorillas_sf$mesh,
    mask = gorillas_sf$boundary,
    col = exp(jfit_joint$summary.random$Difference$mean -
      jfit$summary.random$Difference$mean)
  )
(pl.major + scale_fill_continuous(trans = "log")) +
  (pl.minor + scale_fill_continuous(trans = "log")) &
  theme(legend.position = "right")

LGCPs - Multiple Likelihoods