Skip to contents

Aggregated count models in one dimension

Finn Lindgren

Generated on 2025-05-20

Source: vignettes/aggregated_counts_1d.Rmd
aggregated_counts_1d.Rmd

This tutorial modifies the 1D random fields tutorial to properly handle aggregated counts.

Setting things up

Make a shortcut to a nicer colour scale:

colsc <- function(...) {
  scale_fill_gradientn(
    colours = rev(RColorBrewer::brewer.pal(11, "RdYlBu")),
    limits = range(..., na.rm = TRUE)
  )
}

Get the data

Load the data and rename the countdata object to cd (just because ‘cd’ is less to type than ‘countdata2’.):

data(Poisson2_1D)
cd <- countdata2

Take a look at the count data.

cd
#>            x count exposure
#> 1   2.319888     9 4.639776
#> 2   6.959664    13 4.639776
#> 3  11.599439    11 4.639776
#> 4  16.239215    22 4.639776
#> 5  20.878991    20 4.639776
#> 6  25.518766    19 4.639776
#> 7  30.158542    16 4.639776
#> 8  34.798318     8 4.639776
#> 9  39.438093     4 4.639776
#> 10 44.077869     4 4.639776
#> 11 48.717645     4 4.639776
ggplot(cd) +
  geom_point(aes(x, y = count)) +
  ylim(0, max(cd$count))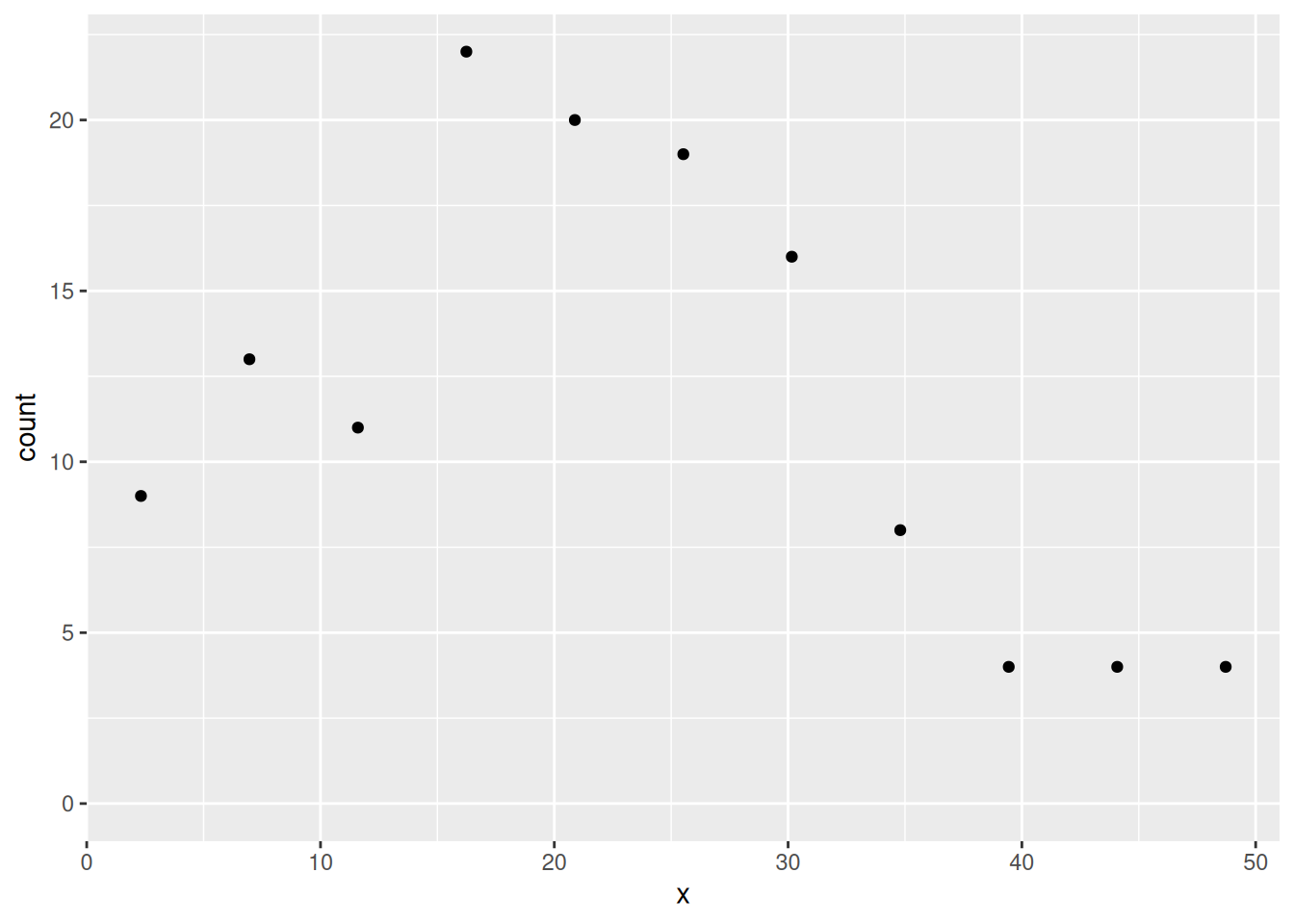

Tip: RStudio > Help > Cheatsheets > Data visualisation with ggplot2 is a useful reference for ggplot2 syntax.

Fitting an SPDE model with inlabru

Make mesh. To avoid boundary effects in the region of interest, let the mesh extend outside the data range.

x <- seq(-10, 65, by = 0.5) # this sets mesh points - try others if you like
(mesh1D <- fm_mesh_1d(x, degree = 2, boundary = "free"))
#> fm_mesh_1d object:
#>   Manifold:  R1
#>   #{knots}:  151
#>   Interval:  (-10,  65)
#>   Boundary:  (free, free)
#>   B-spline degree:   2
#>   Basis d.o.f.:  152

Using function bru( ) to fit to aggregated count data

We need to specify model components and a model formula in order to fit it. This can be done inside the call to bru( ) but that is a bit messy, so we’ll store it in comp first and then pass that to bru( ).

Our response variable in the data frame cd is called count so the model specification needs to have that on the left of the ~. We add an intercept component with + Intercept(1) on the right hand side (all the models we use have intercepts), and because we want to fit a Gaussian random field (GRF), it must have a GRF specification. In inlabru the GRF specification is a function, which allows the GRF to be calculated at any point in space while inlabru is doing its calculations.

The user gets to name the GRF function. The syntax is myname(input, model= ...), where:

  • ‘myname’ is whatever you want to call the GRF (we called it field below);
  • input specifies the coordinates in which the GRF or SPDE ‘lives’. Here we are working in one dimension, and we called that dimension x when we set up the data set.
  • model= designates the type of effect, here an SPDE model object from the INLA function inla.spde2.pcmatern( ), which requires a mesh to be passed to it, so we pass it the 1D mesh that we created above, mesh1D.

For models that only sums all the model components, we don’t need to specify the full predictor formula. Instead, we can provide the name of the output to the left of the ~ in the component specification, and “.” on the right hand side, which will cause it to add all components (unless a subset is selected via the used argument to bru_obs()).

the_spde <- inla.spde2.pcmatern(mesh1D,
  prior.range = c(1, 0.01),
  prior.sigma = c(1, 0.01)
)

comp <- ~ field(x, model = the_spde) + Intercept(1, prec.linear = 1 / 2^2)

Approximate model pretending that the counts are measured at individual points:

fit2.bru <- bru(
  comp,
  bru_obs(
    count ~ .,
    data = cd,
    family = "poisson",
    E = exposure
  )
)

summary(fit2.bru)
#> inlabru version: 2.12.0.9016
#> INLA version: 25.05.18-1
#> Components:
#> field: main = spde(x), group = exchangeable(1L), replicate = iid(1L), NULL
#> Intercept: main = linear(1), group = exchangeable(1L), replicate = iid(1L), NULL
#> Observation models:
#>   Family: 'poisson'
#>     Tag: ''
#>     Data class: 'data.frame'
#>     Response class: 'integer'
#>     Predictor: count ~ .
#>     Additive/Linear: TRUE/TRUE
#>     Used components: effects[field, Intercept], latent[]
#> Time used:
#>     Pre = 0.489, Running = 0.457, Post = 0.0895, Total = 1.04 
#> Fixed effects:
#>            mean    sd 0.025quant 0.5quant 0.975quant  mode kld
#> Intercept 0.626 0.479     -0.437    0.658       1.52 0.729   0
#> 
#> Random effects:
#>   Name     Model
#>     field SPDE2 model
#> 
#> Model hyperparameters:
#>                   mean     sd 0.025quant 0.5quant 0.975quant   mode
#> Range for field 35.074 19.904     10.922   30.470      86.45 23.073
#> Stdev for field  0.594  0.221      0.275    0.557       1.13  0.488
#> 
#> Deviance Information Criterion (DIC) ...............: 59.22
#> Deviance Information Criterion (DIC, saturated) ....: 13.58
#> Effective number of parameters .....................: 5.16
#> 
#> Watanabe-Akaike information criterion (WAIC) ...: 57.43
#> Effective number of parameters .................: 2.63
#> 
#> Marginal log-Likelihood:  -36.69 
#>  is computed 
#> Posterior summaries for the linear predictor and the fitted values are computed
#> (Posterior marginals needs also 'control.compute=list(return.marginals.predictor=TRUE)')

Model that takes into account that the expected counts are integrals:

data_integration <- fm_int(
  mesh1D,
  samplers = with(cd, cbind(x - exposure/2, x + exposure/2))
)
if (packageVersion("inlabru") >= "2.12.0.9016") {
  # From 2.12.0.9016:
  fit2block.bru <- bru(
    comp,
    bru_obs(
      count ~ .,
      data = data_integration,
      response_data = cd,
      aggregate = "logsumexp",
      family = "poisson"
    )
  )
} else {
  # Before 2.12.0.9016:
  fit2block.bru <- bru(
    comp,
    bru_obs(
      count ~ fm_block_logsumexp_eval(
        block = .block,
        weights = weight,
        n_block = NROW(cd),
        values = Intercept + field
      ),
      allow_combine = TRUE,
      data = data_integration,
      response_data = cd,
      family = "poisson"
    )
  )
}

summary(fit2block.bru)
#> inlabru version: 2.12.0.9016
#> INLA version: 25.05.18-1
#> Components:
#> field: main = spde(x), group = exchangeable(1L), replicate = iid(1L), NULL
#> Intercept: main = linear(1), group = exchangeable(1L), replicate = iid(1L), NULL
#> Observation models:
#>   Family: 'poisson'
#>     Tag: ''
#>     Data class: 'tbl_df', 'tbl', 'data.frame'
#>     Response class: 'integer'
#>     Predictor: count ~ .
#>     Additive/Linear: FALSE/FALSE
#>     Used components: effects[field, Intercept], latent[]
#> Time used:
#>     Pre = 0.352, Running = 0.472, Post = 0.0798, Total = 0.905 
#> Fixed effects:
#>            mean    sd 0.025quant 0.5quant 0.975quant  mode kld
#> Intercept 0.627 0.472     -0.419    0.659      1.508 0.729   0
#> 
#> Random effects:
#>   Name     Model
#>     field SPDE2 model
#> 
#> Model hyperparameters:
#>                   mean     sd 0.025quant 0.5quant 0.975quant   mode
#> Range for field 33.590 19.718      9.978   28.954      84.61 21.549
#> Stdev for field  0.595  0.218      0.279    0.559       1.12  0.492
#> 
#> Deviance Information Criterion (DIC) ...............: 59.01
#> Deviance Information Criterion (DIC, saturated) ....: 13.37
#> Effective number of parameters .....................: 5.01
#> 
#> Watanabe-Akaike information criterion (WAIC) ...: 57.28
#> Effective number of parameters .................: 2.57
#> 
#> Marginal log-Likelihood:  -36.58 
#>  is computed 
#> Posterior summaries for the linear predictor and the fitted values are computed
#> (Posterior marginals needs also 'control.compute=list(return.marginals.predictor=TRUE)')

Predict the lambda function (the data argument must be a data frame, see ?predict.bru):

x4pred <- data.frame(x = seq(0, 55, by = 0.1))
pred2.bru <- predict(fit2.bru,
  x4pred,
  x ~ exp(field + Intercept),
  n.samples = 1000
)
pred2block.bru <- predict(fit2block.bru,
  x4pred,
  x ~ exp(field + Intercept),
  n.samples = 1000
)

Let’s do a plot to compare the fitted model to the true model. The true lambda is given by the function lambda2_1D(), and the expected counts of the true model are stored in the variable E_nc2 which comes with the dataset Poisson2_1D. For ease of use in plotting with ggplot2 (which needs a data frame), we create a data frame which we call true.lambda, containing x- and y variables as shown below.

true.lambda <- data.frame(x = x4pred$x, lambda = lambda2_1D(x4pred$x))

These ggplot2 commands should generate the plot shown below. It shows the true intensities as a blue line, the observed intensities as black dots, and the fitted intensity function as a red curve, with 95% credible intervals shown as a light bands about the curves.

ggplot() +
  gg(pred2.bru) +
  gg(pred2block.bru,mapping = aes(fill="red"), alpha=0.2, color = "red") +
  geom_point(data = cd, aes(x = x, y = count / exposure), cex = 2) +
  geom_line(data = true.lambda, aes(x, lambda), col = "blue") +
  coord_cartesian(xlim = c(0, 55), ylim = c(0, 6)) +
  xlab("x") +
  ylab("Intensity")
#> Warning in ggplot2::geom_line(data = data, line.map, ...): Ignoring
#> unknown aesthetics: fill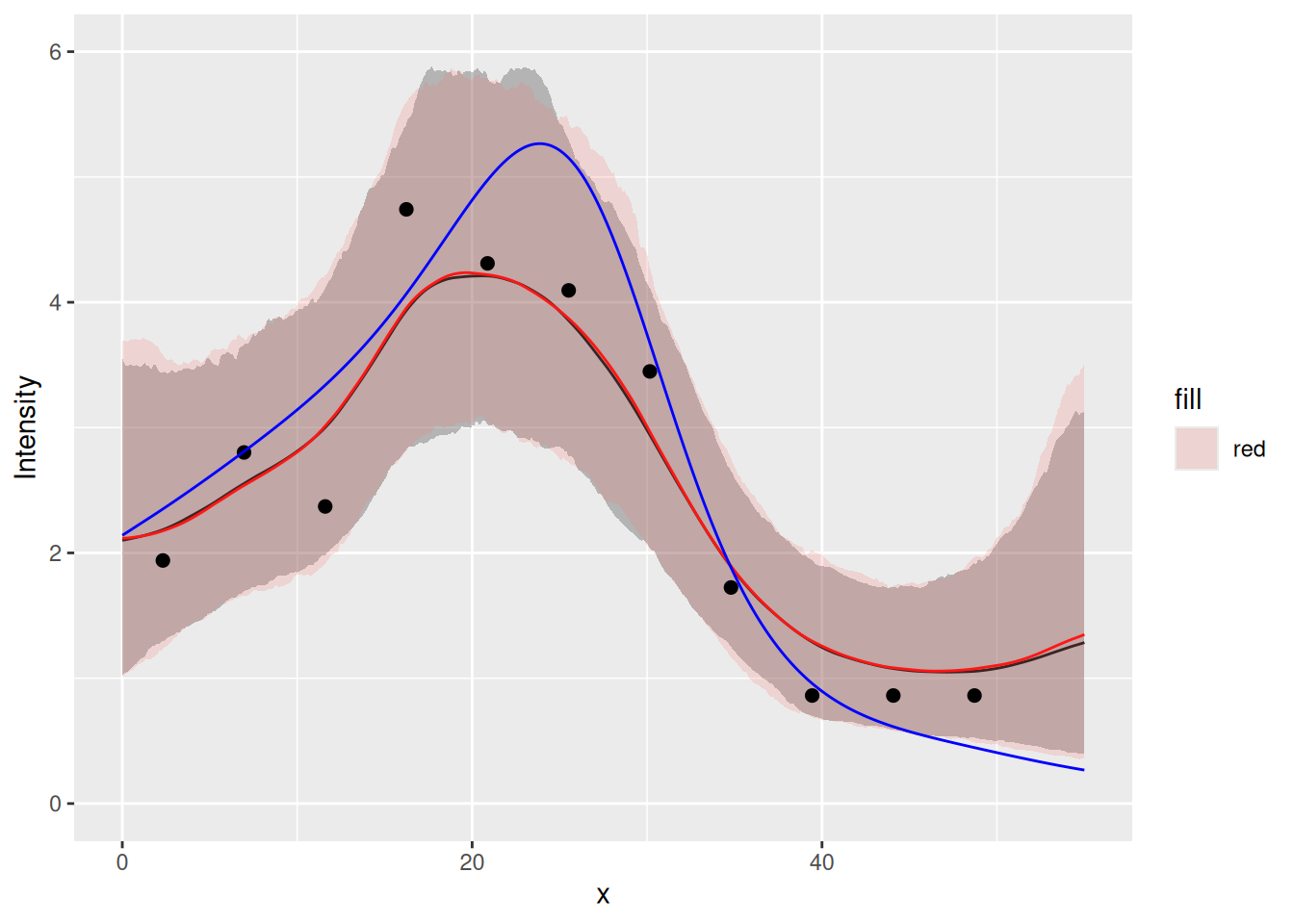

We can see that for this toy problem, using the proper aggregated count observation model doesn’t make a noticeable difference to the fitted model. For more realistic settings, in particular those involving high resolution covariates, the distinction becomes important, and the the integration scheme to resolve small features.

The computational time is available from bru_timings():

bru_timings(fit2.bru)
#>         Task Iteration       Time     System    Elapsed
#> 1 Preprocess         0 0.386 secs 0.019 secs 0.392 secs
#> 2 Preprocess         1 0.102 secs 0.018 secs 0.111 secs
#> 3 Run inla()         1 0.983 secs 0.144 secs 1.065 secs
bru_timings(fit2block.bru)
#>          Task Iteration       Time     System    Elapsed
#> 1  Preprocess         0 0.099 secs 0.030 secs 0.117 secs
#> 2  Preprocess         1 0.203 secs 0.000 secs 0.203 secs
#> 3  Run inla()         1 0.672 secs 0.088 secs 0.776 secs
#> 4 Line search         1 0.014 secs 0.000 secs 0.014 secs
#> 5  Preprocess         2 0.208 secs 0.000 secs 0.208 secs
#> 6  Run inla()         2 0.706 secs 0.056 secs 0.777 secs
#> 7 Line search         2 0.230 secs 0.000 secs 0.230 secs
#> 8  Preprocess         3 0.166 secs 0.002 secs 0.167 secs
#> 9  Run inla()         3 0.915 secs 0.058 secs 0.928 secs
bru_timings_plot(fit2block.bru)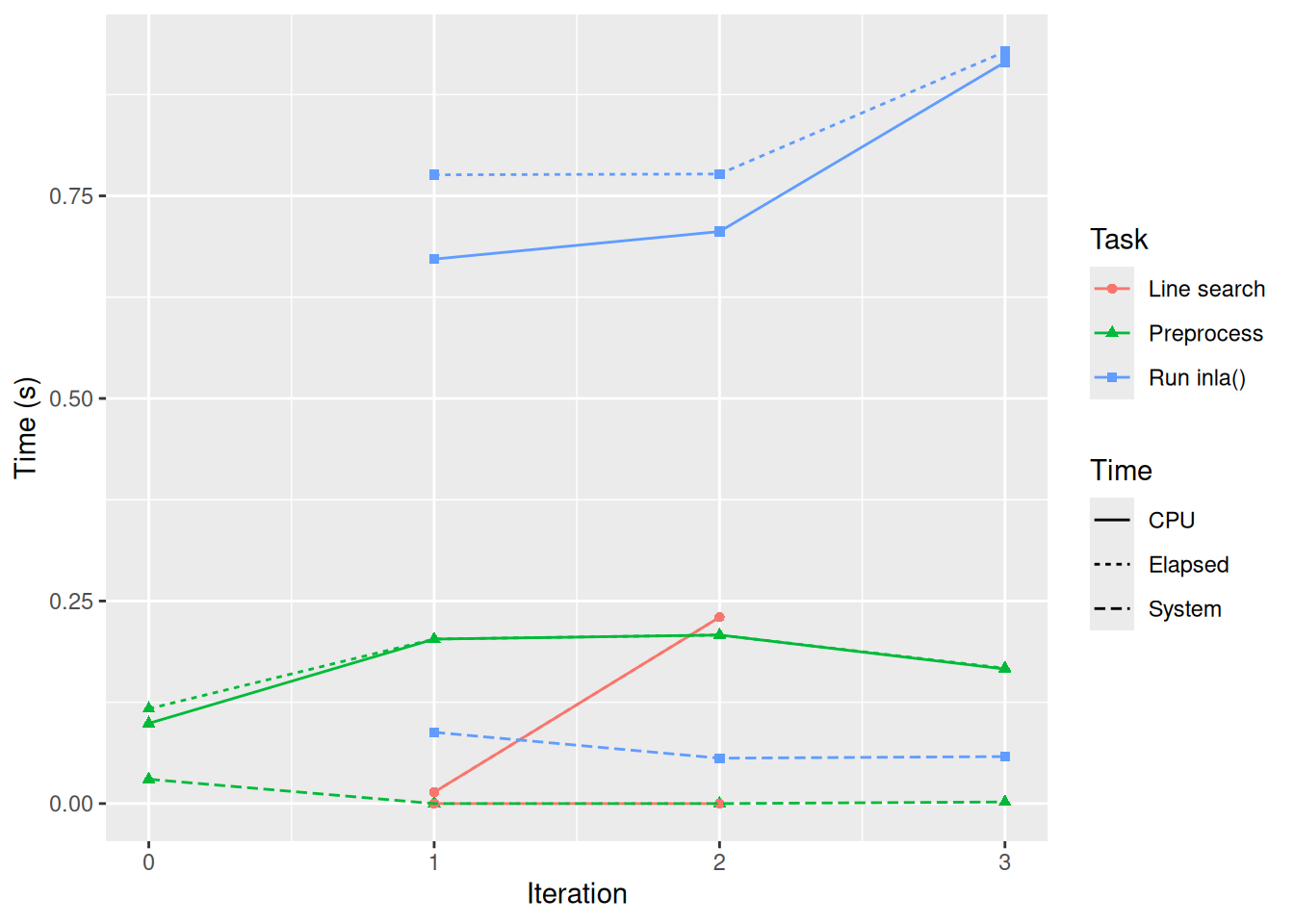

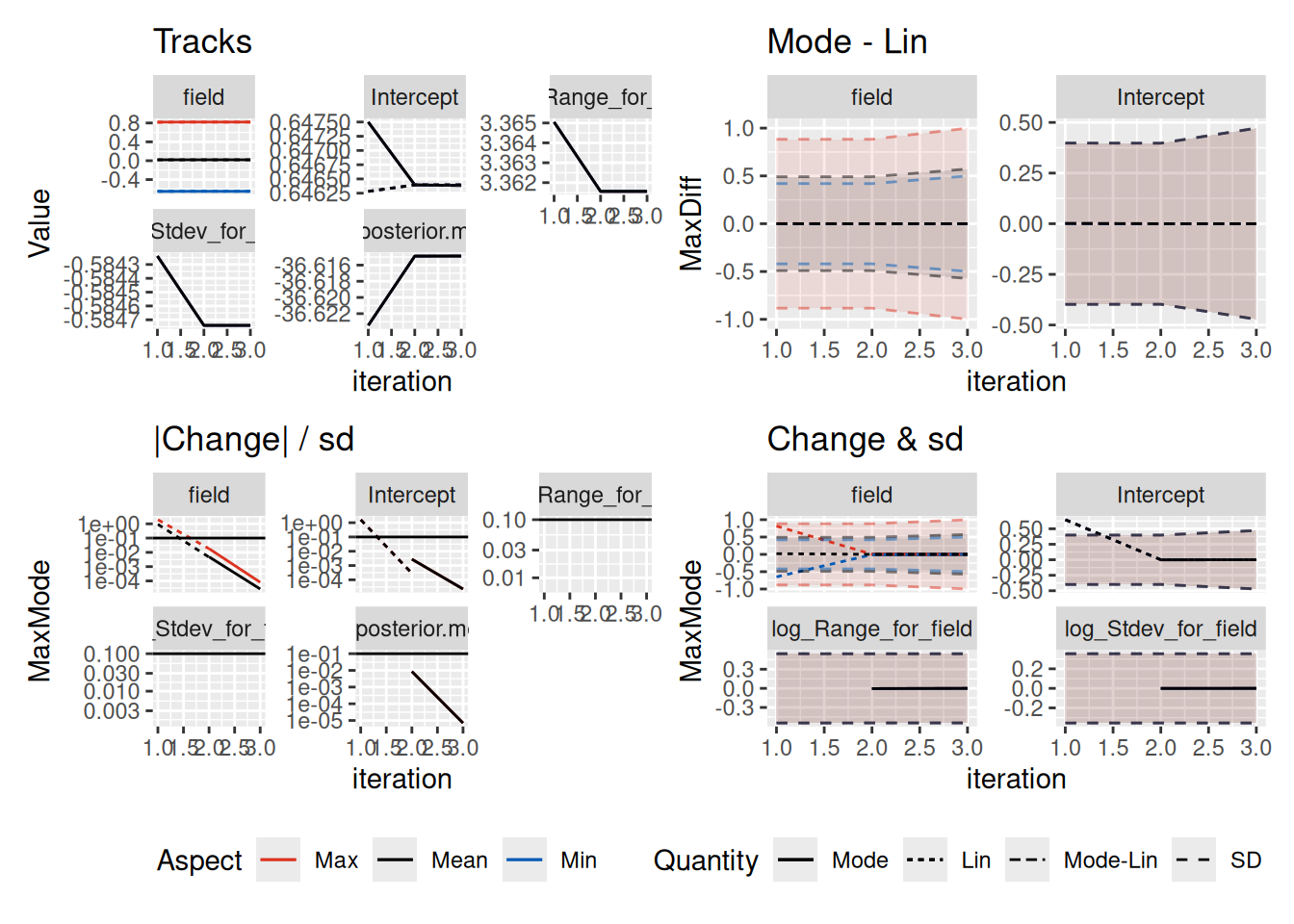
To check the iterative method convergence, use bru_convergence_plot():

bru_convergence_plot(fit2block.bru)