The Integrated nested Laplace approximation for fitting Dirichlet regression models

Introduction

This vignette is devoted to explain how to use the package dirinla. It is a R-package to fit Dirichlet regression models using R-INLA. It can be installed and upgraded via the repository https://github.com/inlabru-org/dirinla. In this manual, we simulate some data from a Dirichlet distribution to posteriorly fit them using the main function of the package dirinla.

library(dirinla)
library(INLA)
library(DirichletReg)
library(ggplot2)
library(gridExtra)

Simulation

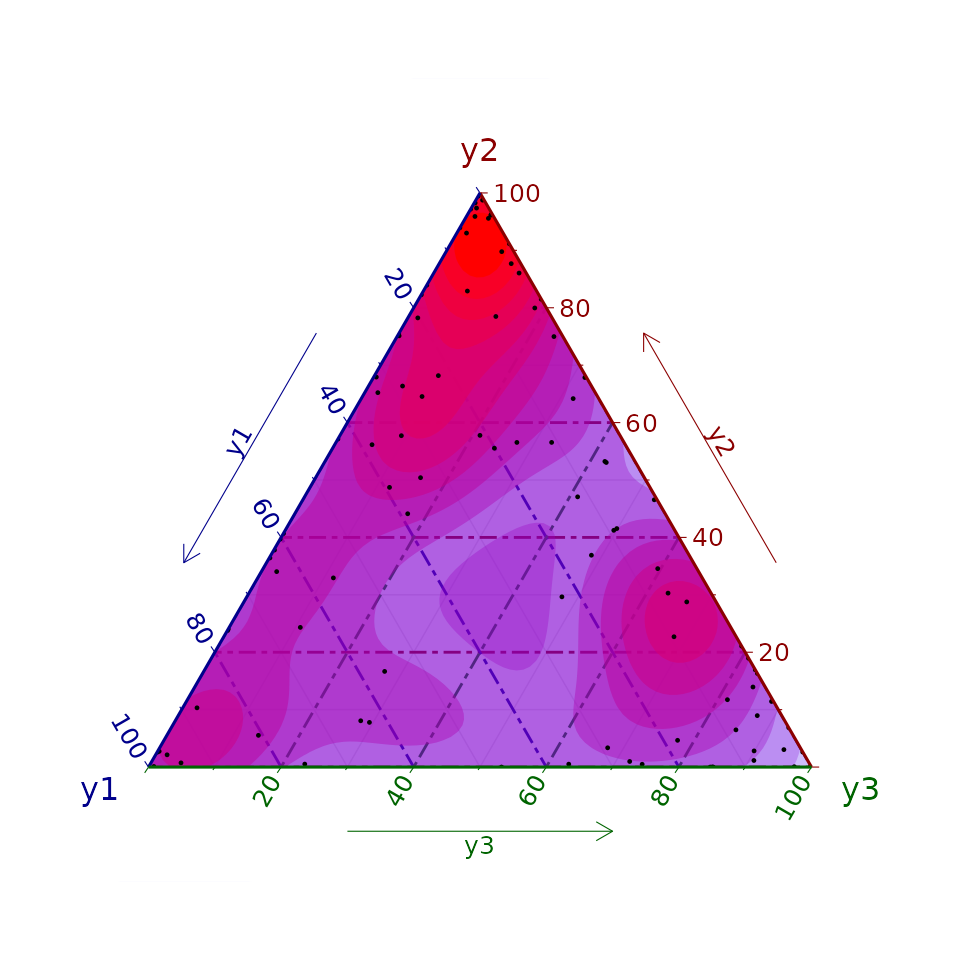
We firstly illustrate how to simulate 100 data points from a Dirichlet regression model with three different categories and one different covariate per category: $\begin{align} \boldsymbol{Y}_n & \sim \text{Dirichlet}(\alpha_{1n}, \ldots, \alpha_{3n}) \,, n = 1, \ldots, 100, \nonumber \\ \log(\alpha_{1n}) & = \beta_{01} + \beta_{11} v_{1n}, \nonumber \\ \log(\alpha_{2n}) & = \beta_{02} + \beta_{12} v_{2n}, \\ \log(\alpha_{3n}) & = \beta_{03} + \beta_{13} v_{3n}, \nonumber \end{align}$ being the parameters that compose the latent field $\beta_{01}= -1.5$ , $\beta_{02}=-2$ , $\beta_{03}=0$ (the intercepts), and $\beta_{11}=1$ , $\beta_{12}=2.3$ , $\beta_{13}=-1.9$ (the slopes). Note that covariates are different for each category. This could be particularized for a situation where all of them are the same. For simplicity, covariates are simulated from a Uniform distribution on (0,1). To posteriorly fit the model, a following the structure of LGMs, Gaussian prior distributions are assigned with precision $10^{-4}$ to all the elements of the Gaussian field.

### --- 2. Simulating from a Dirichlet likelihood --- ####
set.seed(1000)
N <- 100 #number of data
V <- as.data.frame(matrix(runif((4) * N, 0, 1), ncol = 4)) #Covariates
names(V) <- paste0('v', 1:4)

formula <- y ~ 1 + v1 | 1 + v2 | 1 + v3
(names_cat <- formula_list(formula))

intercepts <-
x <- c(-1.5, 1, #Cat 1
       -2, 2.3, #Cat 2
       0 , -1.9) #Cat 3

mus <- exp(x) / sum(exp(x))
C <- length(names_cat)
data_stack_construct <-
  data_stack_dirich(y = as.vector(rep(NA, N * C)),
                    covariates = names_cat,
                    data       = V,
                    d          = C,
                    n          = N)

A_construct <- data_stack_construct
A_construct[1:8, ]

eta <- A_construct %*% x
alpha <- exp(eta)
alpha <- matrix(alpha,
                ncol  = C,
                byrow = TRUE)
y_o <- rdirichlet(N, alpha)
colnames(y_o) <- paste0("y", 1:C)
head(y_o)

Fitting the model

The next step is to call the dirinlareg function in order to fit a model to the data. We just need to specify the formula, the response variable, the covariates and the precision for the Gaussian prior distribution of the parameters.

### --- 3. Fitting the model --- ####
y <- y_o
model.inla <- dirinlareg(
  formula  = y ~ 1 + v1 | 1 + v2 | 1 + v3,
  y        = y,
  data.cov = V,
  prec     = 0.0001,
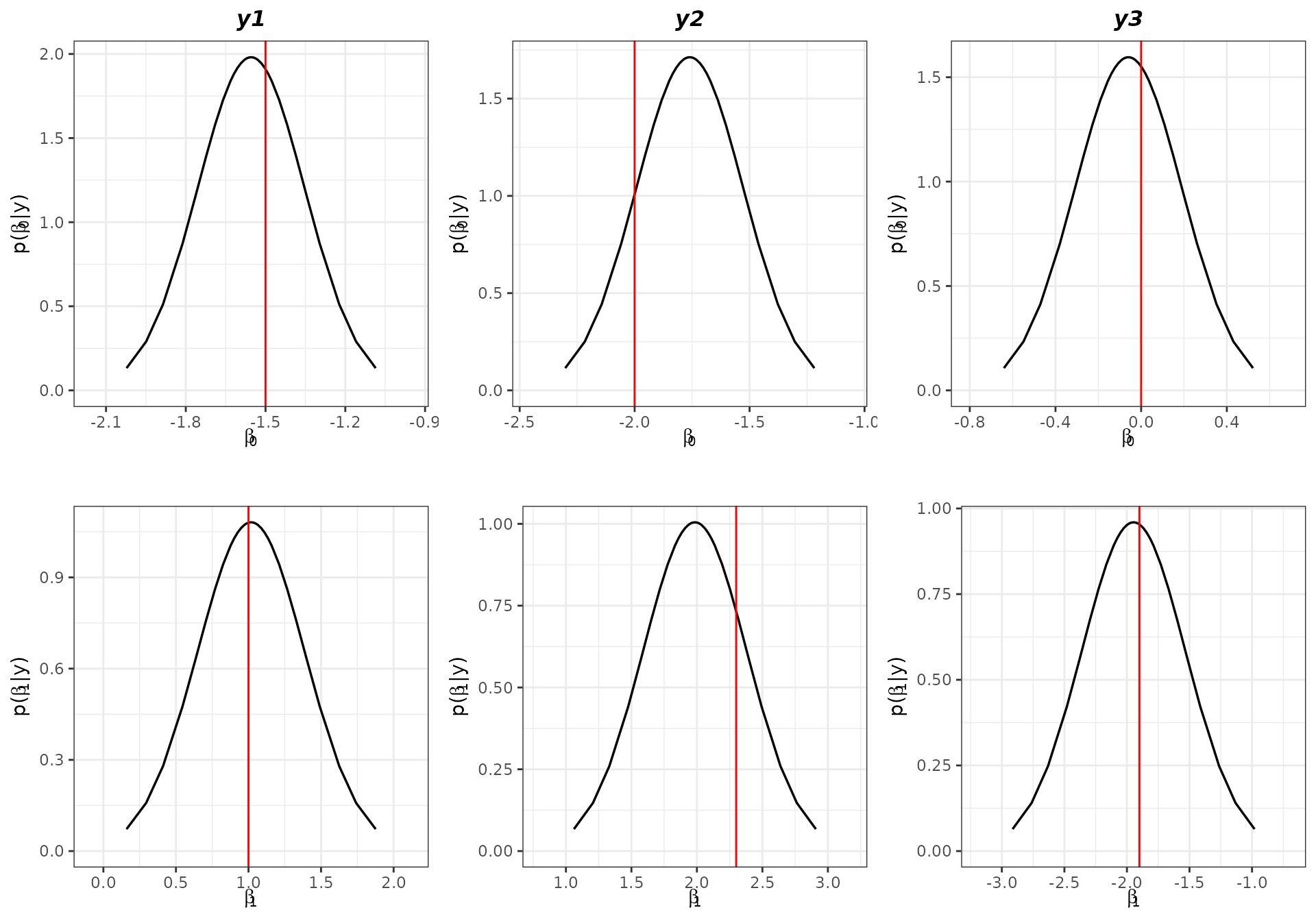
  verbose  = TRUE)

To collect information about the fitted values and marginal posterior distributions of the parameters, we can use the methods summary and plot directly to the dirinlaregmodel object generated.

Summary

summary(model.inla)
#> 
#> Call: 
#>  dirinlareg(formula = y ~ 1 + v1 | 1 + v2 | 1 + v3, y = y, data.cov = V, 
#>     prec = 1e-04, verbose = TRUE)
#> 
#>  
#> ---- FIXED EFFECTS ---- 
#> ======================================================================= 
#> y1
#> ----------------------------------------------------------------------- 
#>             mean     sd 0.025quant 0.5quant 0.975quant   mode
#> intercept -1.554 0.2014    -1.9490   -1.554     -1.159 -1.554
#> v1         1.018 0.3690     0.2948    1.018      1.741  1.018
#> ======================================================================= 
#> y2
#> ----------------------------------------------------------------------- 
#>             mean     sd 0.025quant 0.5quant 0.975quant   mode
#> intercept -1.760 0.2329     -2.217   -1.760     -1.304 -1.760
#> v2         1.985 0.3971      1.206    1.985      2.763  1.985
#> ======================================================================= 
#> y3
#> ----------------------------------------------------------------------- 
#>               mean     sd 0.025quant 0.5quant 0.975quant     mode
#> intercept -0.05927 0.2500    -0.5493 -0.05927     0.4307 -0.05927
#> v3        -1.94703 0.4158    -2.7619 -1.94703    -1.1322 -1.94703
#> ======================================================================= 
#> 
#> ---- HYPERPARAMETERS ---- 
#> 
#>  No hyperparameters in the model 
#> ======================================================================= 
#> DIC = 1821.0264 , WAIC = 1711.0295 , LCPO = 913.8332 
#> Number of observations: 100
#> Number of Categories: 3

Plot of the posterior distributions

Posterior predictive distribution in the simplex. Points represent the original data

Posterior distributions of the parameters. Vertical line represents the real value

Predictions

The package provides a method predict to compute posterior predictive distributions for new individuals. To show how this function works, we will predict for a value of v1 = 0.2, v2 = 0.5, and v3 = -0.1:

### --- 5. Predicting for v1 = 0.25, v2 = 0.5, v3 = 0.5, v4 = 0.1 --- ####
model.prediction <-
  predict(model.inla,
                  data.pred.cov = data.frame(v1 = 0.2 ,
                                         v2 = 0.5,
                                         v3 = -0.1))
#> 
#>  
#>  ---------------------- Predicting ----------------- 
#>  
#> 
model.prediction$summary_predictive_means
#> $y1
#>            Min.   1st Qu.    Median      Mean   3rd Qu.      Max.
#> [1,] 0.05081676 0.1148319 0.1372829 0.1405741 0.1619588 0.3298339
#> 
#> $y2
#>            Min.  1st Qu.    Median      Mean   3rd Qu.      Max.
#> [1,] 0.07885047 0.203052 0.2470197 0.2529631 0.2966277 0.5925871
#> 
#> $y3
#>           Min.   1st Qu.    Median      Mean   3rd Qu.      Max.
#> [1,] 0.3085924 0.5549312 0.6094127 0.6064628 0.6599187 0.8312106

### --- 6. We can also predict directly --- ####
model.inla <- dirinlareg(
  formula  = y ~ 1 + v1 | 1 + v2 | 1 + v3,
  y        = y,
  data.cov = V,
  prec     = 0.0001,
  verbose  = FALSE,
  prediction = TRUE,
  data.pred.cov = data.frame(v1 = 0.2 ,
                             v2 = 0.5,
                             v3 = -0.1))
#> 
#>  
#>  ---------------------- Looking for the mode ----------------- 
#>  
#>  
#>  ----------------------    INLA call    ----------------- 
#> 
#>  ---------------------- Obtaining linear predictor ----------------- 
#> 
#>  
#>  ---------------------- Predicting ----------------- 
#>  
#> 


model.prediction$summary_predictive_means
#> $y1
#>            Min.   1st Qu.    Median      Mean   3rd Qu.      Max.
#> [1,] 0.05081676 0.1148319 0.1372829 0.1405741 0.1619588 0.3298339
#> 
#> $y2
#>            Min.  1st Qu.    Median      Mean   3rd Qu.      Max.
#> [1,] 0.07885047 0.203052 0.2470197 0.2529631 0.2966277 0.5925871
#> 
#> $y3
#>           Min.   1st Qu.    Median      Mean   3rd Qu.      Max.
#> [1,] 0.3085924 0.5549312 0.6094127 0.6064628 0.6599187 0.8312106