Split triangles of a mesh into subtriangles — fm

Splits each mesh triangle into (n + 1)^2 subtriangles. The current version drops any edge constraint information from the mesh.

Usage

fm_subdivide(mesh, n = 1, delaunay = FALSE)

Arguments

mesh: an fm_mesh_2d object
n: number of added points along each edge. Default is 1.
delaunay: logical; if TRUE, the subdivided mesh is forced into a Delaunay triangle structure. If FALSE (default), the triangles are subdivided uniformly instead.

Value

A refined fm_mesh_2d object, with added bary information (an fm_bary() object), that can be used for interpolating functions from the original mesh to the new mesh (from version 0.5.0.9002).

Author

Finn Lindgren Finn.Lindgren@gmail.com

Examples

mesh <- fm_rcdt_2d_inla(
  loc = rbind(c(0, 0), c(1, 0), c(0, 1)),
  tv = rbind(c(1, 2, 3))
)
mesh_sub <- fm_subdivide(mesh, 3)
mesh
#> fm_mesh_2d object:
#>   Manifold:	R2
#>   V / E / T:	3 / 3 / 1
#>   Euler char.:	1
#>   Constraints:	Boundary: 3 boundary edges (1 group: 0), Interior: 0 edges
#>   Bounding box: (0,1) x (0,1)
#>   Basis d.o.f.:	3
mesh_sub
#> fm_mesh_2d object:
#>   Manifold:	R2
#>   V / E / T:	15 / 30 / 16
#>   Euler char.:	1
#>   Constraints:	Boundary: 12 boundary edges (1 group: 0), Interior: 0 edges
#>   Bounding box: (0,1) x (0,1)
#>   Basis d.o.f.:	15

# Difference should be zero for flat triangle meshes:
sum((mesh_sub$loc - fm_basis(mesh, mesh_sub$bary) %*% mesh$loc)^2)
#> [1] 0

plot(mesh_sub, edge.color = 2)


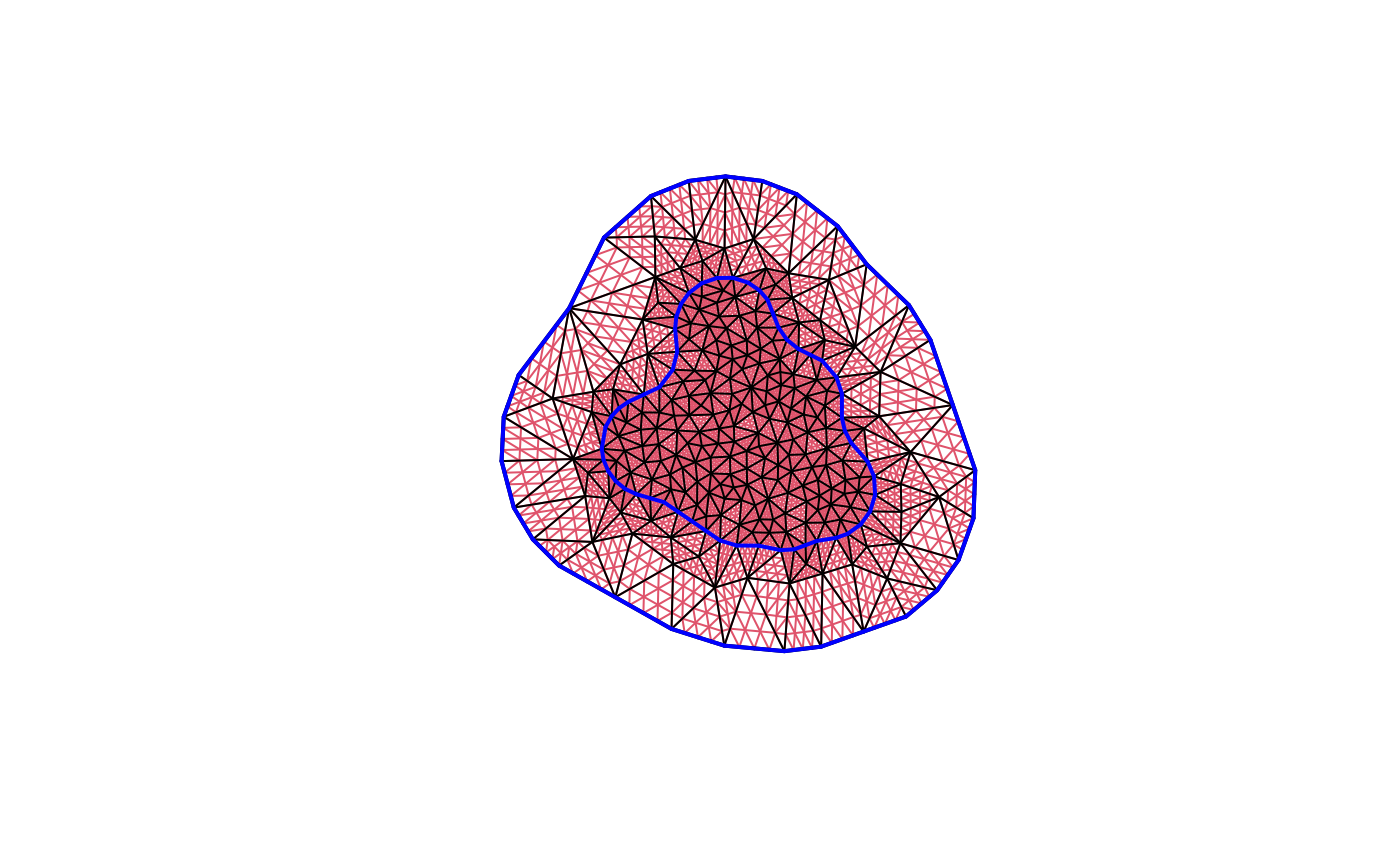
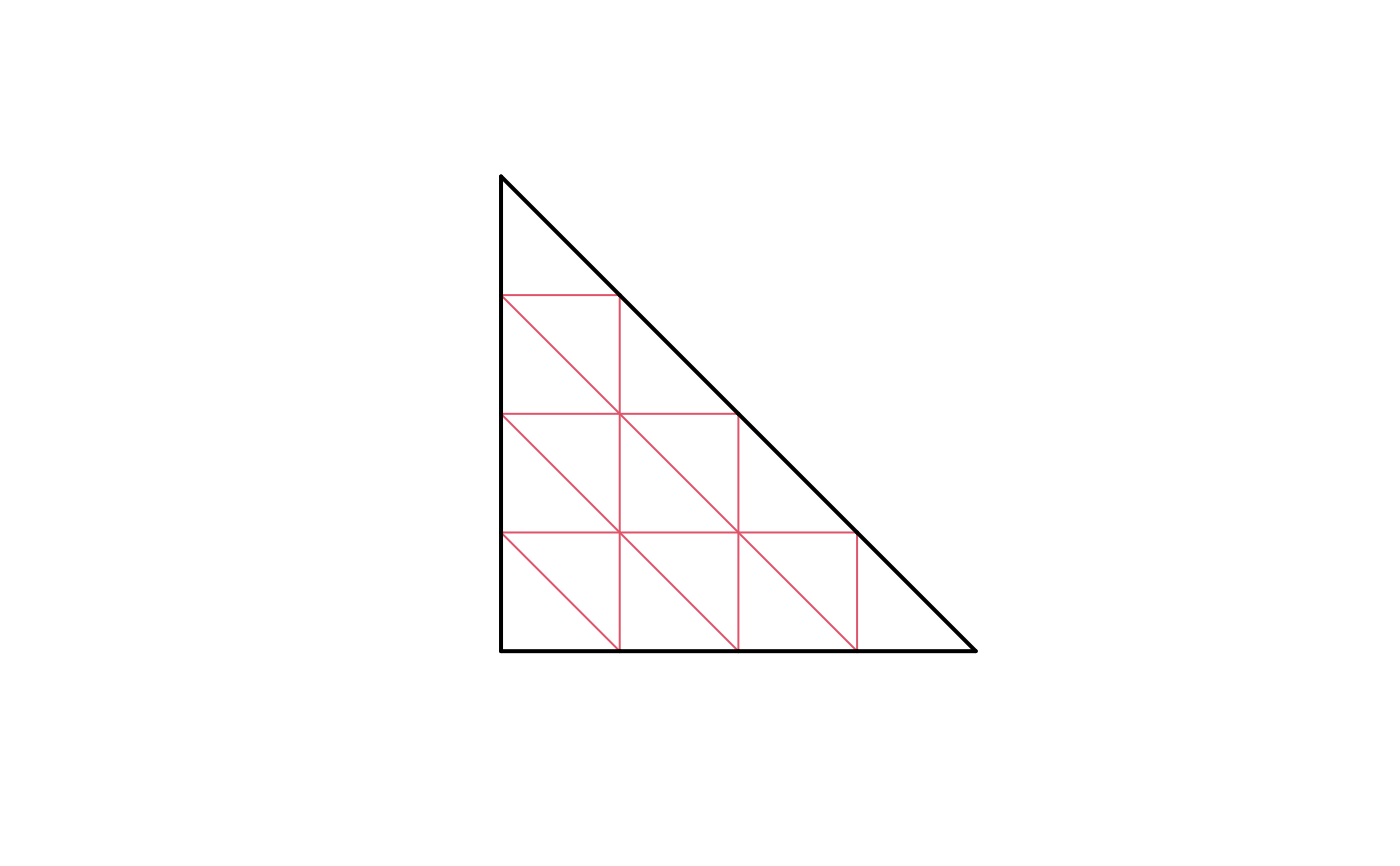plot(fm_subdivide(fmexample$mesh, 3), edge.color = 2)
plot(fmexample$mesh, add = TRUE, edge.color = 1)