Basis functions for mesh manifolds

Calculate basis functions on fm_mesh_1d() or fm_mesh_2d(), without necessarily matching the default function space of the given mesh object.

Usage

fm_raw_basis(
  mesh,
  type = "b.spline",
  n = 3,
  degree = 2,
  knot.placement = "uniform.area",
  rot.inv = TRUE,
  boundary = "free",
  free.clamped = TRUE,
  ...
)

Arguments

mesh

An fm_mesh_1d() or fm_mesh_2d() object.

type

b.spline (default) for B-spline basis functions, sph.harm for spherical harmonics (available only for meshes on the sphere)

n

For B-splines, the number of basis functions in each direction (for 1d meshes n must be a scalar, and for planar 2d meshes a 2-vector). For spherical harmonics, n is the maximal harmonic order.

degree

Degree of B-spline polynomials. See fm_mesh_1d().

knot.placement

For B-splines on the sphere, controls the latitudinal placements of knots. "uniform.area" (default) gives uniform spacing in sin(latitude), "uniform.latitude" gives uniform spacing in latitudes.

rot.inv

For spherical harmonics on a sphere, rot.inv=TRUE gives the rotationally invariant subset of basis functions.

boundary

Boundary specification, default is free boundaries. See fm_mesh_1d() for more information.

free.clamped

If TRUE and boundary is "free", the boundary basis functions are clamped to 0/1 at the interval boundary by repeating the boundary knots. See fm_mesh_1d() for more information.

...

Unused

Value

A matrix with evaluated basis function

See also

fm_mesh_1d(), fm_mesh_2d(), fm_basis()

Author

Finn Lindgren finn.lindgren@gmail.com

Examples

loc <- rbind(c(0, 0), c(1, 0), c(1, 1), c(0, 1))
mesh <- fm_mesh_2d(loc, max.edge = 0.15)
basis <- fm_raw_basis(mesh, n = c(4, 5))

proj <- fm_evaluator(mesh, dims = c(10, 10))
image(proj$x, proj$y, fm_evaluate(proj, basis[, 7]), asp = 1)

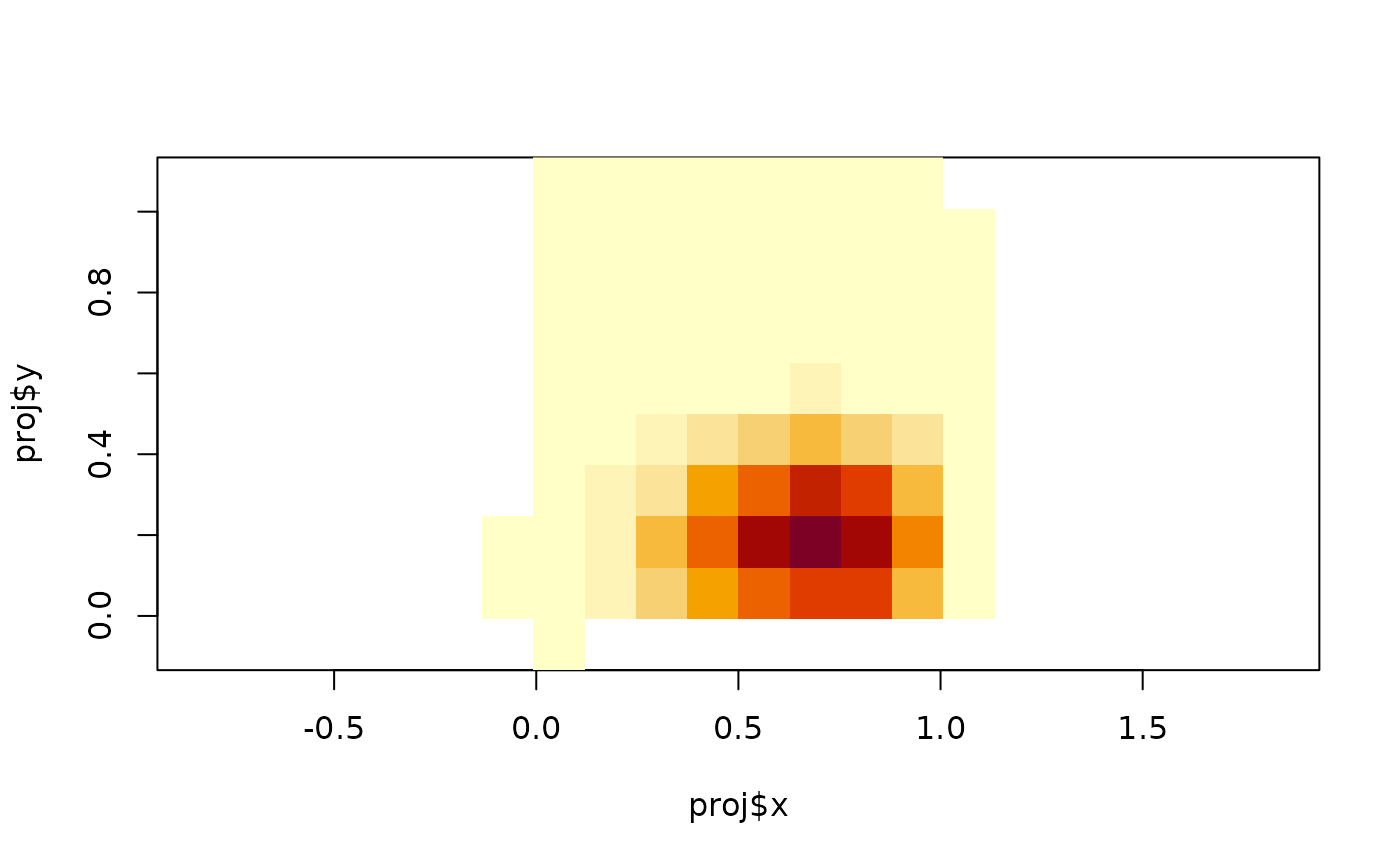# \donttest{
if (interactive() && require("rgl")) {
  plot_rgl(mesh, col = basis[, 7], draw.edges = FALSE, draw.vertices = FALSE)
}
# }