Compute an extension of a spatial object

Constructs a potentially nonconvex extension of a spatial object by performing dilation by convex + concave followed by erosion by concave. This is equivalent to dilation by convex followed by closing (dilation + erosion) by concave.

Usage

fm_nonconvex_hull(x, ..., format = "sf", method = "fm")

fm_extensions(
  x,
  convex = -0.15,
  concave = convex,
  ...,
  format = "sf",
  method = "fm"
)

fm_nonconvex_hull_fm(
  x,
  convex = -0.15,
  concave = convex,
  resolution = 40,
  eps = NULL,
  eps_rel = NULL,
  crs = fm_crs(x),
  ...
)

fm_nonconvex_hull_sf(
  x,
  convex = -0.15,
  concave = convex,
  preserveTopology = TRUE,
  dTolerance = NULL,
  crs = fm_crs(x),
  ...
)

# S3 method for class 'sfc'
fm_nonconvex_hull(x, ..., format = "sf", method = "fm")

# S3 method for class 'matrix'
fm_nonconvex_hull(x, ..., format = "sf", method = "fm")

# S3 method for class 'sf'
fm_nonconvex_hull(x, ..., format = "sf", method = "fm")

# S3 method for class 'Spatial'
fm_nonconvex_hull(x, ..., format = "sf", method = "fm")

# S3 method for class 'sfg'
fm_nonconvex_hull(x, ..., format = "sf", method = "fm")

# S3 method for class 'fm_segm'
fm_nonconvex_hull(x, ..., format = "sf", method = "fm")

# S3 method for class 'fm_segm_list'
fm_nonconvex_hull(x, ..., format = "sf", method = "fm")

Arguments

x: A spatial object
...: Arguments passed on to the fm_nonconvex_hull() sub-methods
format: character specifying the output format; "sf" (default) or "fm"
method: character specifying the construction method; "fm" (default) or "sf"
convex: numeric vector; How much to extend
concave: numeric vector; The minimum allowed reentrant curvature. Default equal to convex
resolution: integer; The internal computation resolution. A warning will be issued when this needs to be increased for higher accuracy, with the required resolution stated. For method="fm" only.
eps, eps_rel: The polygonal curve simplification tolerances used for simplifying the resulting boundary curve. See fm_simplify_helper() for details. For method="fm" only.
crs: Optional crs object for the resulting polygon. Default is fm_crs(x)
preserveTopology: logical; argument to sf::st_simplify() (for method="sf" only)
dTolerance: If not zero, controls the dTolerance argument to sf::st_simplify(). The default is pmin(convex, concave) / 40, chosen to give approximately 4 or more subsegments per circular quadrant. (for method="sf" only)

Value

fm_nonconvex_hull() returns an extended object as an sfc polygon object (if format = "sf") or an fm_segm object (if `format = "fm")

fm_extensions() returns a list of sfc objects.

Details

Morphological dilation by convex, followed by closing by concave, with minimum concave curvature radius concave. If the dilated set has no gaps of width between $$2 \textrm{convex} (\sqrt{1+2\textrm{concave}/\textrm{convex}} - 1) $$ and $2\textrm{concave}$, then the minimum convex curvature radius is convex.

The implementation is based on the identity $$\textrm{dilation}(a) \& \textrm{closing}(b) = \textrm{dilation}(a+b) \& \textrm{erosion}(b)$$ where all operations are with respect to disks with the specified radii.

When convex, concave, or dTolerance are negative, fm_diameter * abs(...) is used instead.

Functions

fm_extensions(): Constructs a potentially nonconvex extension of a spatial object by performing dilation by convex + concave followed by erosion by concave. This is equivalent to dilation by convex followed by closing (dilation + erosion) by concave.

The ... arguments are passed on to fm_nonconvex_hull_fm() or fm_nonconvex_hull_sf(), depending on the method argument.
fm_nonconvex_hull_fm(): fmesher method for fm_nonconvex_hull(), which uses the splancs::nndistF() function to compute nearest-neighbour distances.
fm_nonconvex_hull_sf(): Differs from sf::st_buffer(x, convex) followed by sf::st_concave_hull() (available from GEOS 3.11) in how the amount of allowed concavity is controlled.

INLA compatibility

For mesh and curve creation, the fm_rcdt_2d_inla(), fm_mesh_2d_inla(), and fm_nonconvex_hull_inla() methods will keep the interface syntax used by INLA::inla.mesh.create(), INLA::inla.mesh.2d(), and INLA::inla.nonconvex.hull() functions, respectively, whereas the fm_rcdt_2d(), fm_mesh_2d(), and fm_nonconvex_hull() interfaces may be different, and potentially change in the future.

References

Gonzalez and Woods (1992), Digital Image Processing

Examples

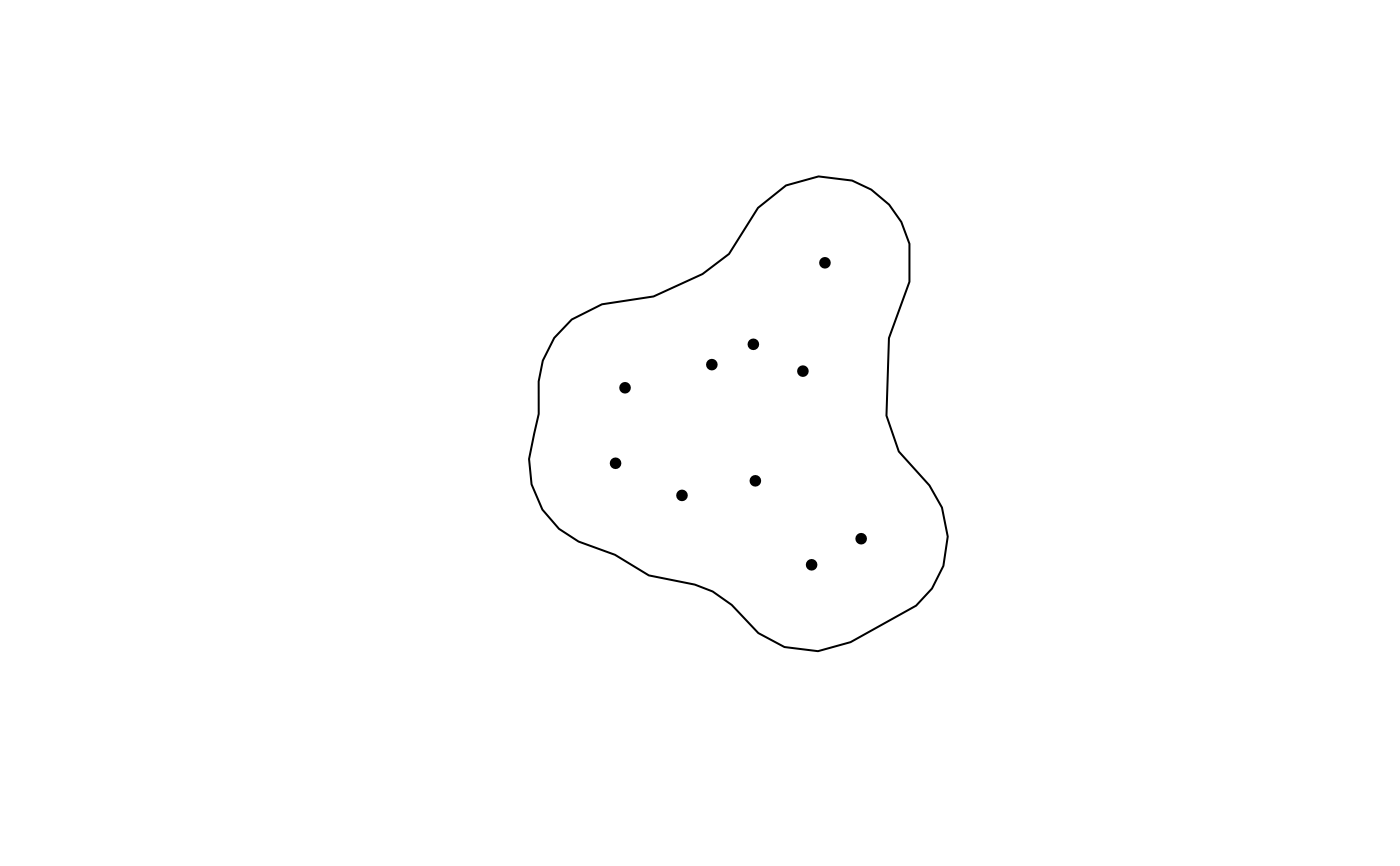
inp <- matrix(rnorm(20), 10, 2)
out <- fm_nonconvex_hull(inp, convex = 1, method = "sf")
plot(out)
points(inp, pch = 20)

out <- fm_nonconvex_hull(inp, convex = 1, method = "fm", format = "fm")
lines(out, col = 2, add = TRUE)

if (TRUE) {
  inp <- sf::st_as_sf(as.data.frame(matrix(1:6, 3, 2)), coords = 1:2)
  bnd <- fm_extensions(inp, convex = c(0.75, 2))
  plot(fm_mesh_2d(boundary = bnd, max.edge = c(0.25, 1)), asp = 1)
}